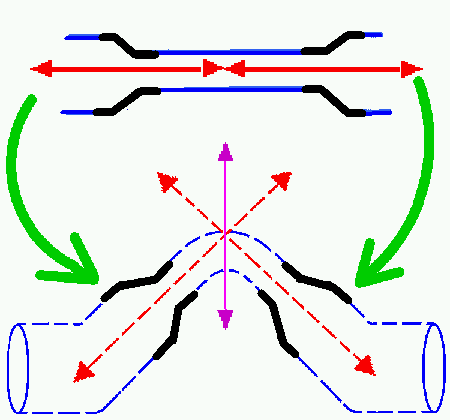
Petit exercice de calcul de contraintes dans une tuyauterie coudée.

Sur la page: la portance 3, il est dit qu'une succession de coudes comme celle-ci:

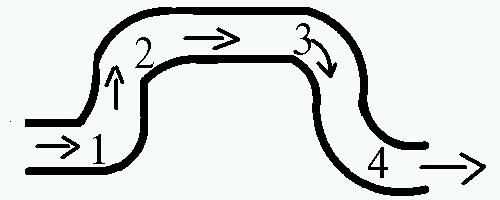
ne produit aucune force résultante assimilable à une portance parce que les efforts produit dans chacun des quatre coudes s'annulent mutuellement.

Les efforts en 1 sont annulés en 2, et les efforts en 3 sont annulés en 4.

Dans l'exemple ci dessus, le diamètre du tuyau est constant, et par conséquent la vitesse d'écoulement du fluide est, elle aussi, constante.

Que se passerait-il si la section de la partie supérieure était plus petite (ce qui produirait une augmentation locale de la vitesse du fluide)?

En d'autre termes, que se passerait-il si la vitesse d'écoulement était plus grande dans la partie supérieure (comme sur une aile)?

La vitesse plus grande ne devrait-elle pas entraîner des contraintes plus importantes vers le haut, et donc une sorte de portance, et cela même si l'écoulement, en sortie, a la même vitesse et la même orientation qu'à l'entrée?

La meilleure façon de s'en assurer, c'est de vérifier. Alors: vérifions donc....
Pour cela, nous utiliserons un système de coudes comme celui-ci:

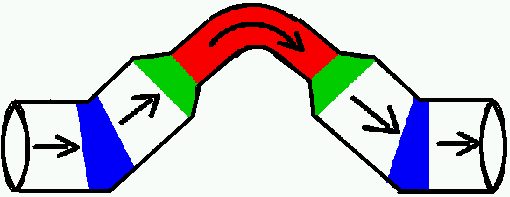
Le système se compose d'un segment horizontal suivi d'un coude (en bleu) tournant vers le haut suivant un angle de 45°.

On trouve ensuite un convergent (en vert) réduisant la section d'origine de moitié.

Lui-même suivi d'un coude (en rouge) de 90° faisant redescendre la canalisation suivant un angle de 45°.

On trouve alors un divergent (en vert) pour retrouver la section de départ.

Et enfin un dernier coude de 45° (en bleu) pour retrouver l'horizontalité parfaite.

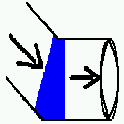
Bilan: l'air entre et sort du système avec exactement la même vitesse et la même orientation, ce qui implique une variation globale de quantité de mouvement nulle donc, théoriquement, une résultante des forces nulle.

Cette affirmation étant niée par certains, nous allons vérifier cela en détail.

Prenons donc un système de tuyaux coudés comme décrit ci dessus, faisons y circuler un fluide (de l'air, par exemple), et calculons le bilan des forces éxercées sur les parois par les changements de direction et de vitesse du fluide.

Pour la facilité, nous commencerons avec des exemples chiffrés.

Le système sera parcouru par un flux d'air d'un débit massique de 30 Kg/sec.

La pression totale à l'intérieur est de 100.000 Pa.

La pression atmosphérique (à l'extérieur) est, elle aussi, de 100.000 Pa.

La vitesse de l'écoulement à l'entrée et à la sortie du système est de 20 m/s.

La vitesse dans la section étroite (coude à 90°, couleur rouge) est de 40 m/s (section deux fois plus petite, donc vitesse deux fois plus grande pour conserver le même débit.

Pour assurer un débit de 30 Kg/s dans les parties larges, en sachant que la masse volumique de l'air est de 1,225 Kg/m³, et que l'écoulement se fait à 20 m/s, il faut une section de 1,22 m².

La section de la partie étroite est deux fois plus petite, et vaut donc 0,61 m².

Pour éviter de devoir tenir compte des forces de frottement, on admet que le fluide est parfait.

La pression totale (Pt) est égale à la pression statique (Ps) + la pression dynamique (Pd), donc: Pt = Ps + 1/2 rho V², donc: Ps = Pt - 1/2 rho V² = 100.000 - (1/2*1,225*20²) = 99.755pa.
La pression statique intérieure dans les parties larges est donc inférieure à la pression statique extérieure (pression atmosphérique), et la pression relative vaut donc: 99.755 - 100.000 = -245 Pa.

De la même façon, on trouve une pression statique de 99.020 Pa dans la partie étroite (coude à 90° rouge) donnant une pression relative de -980 Pa.

1) Contraintes sur les coudes à 45° (en bleu).

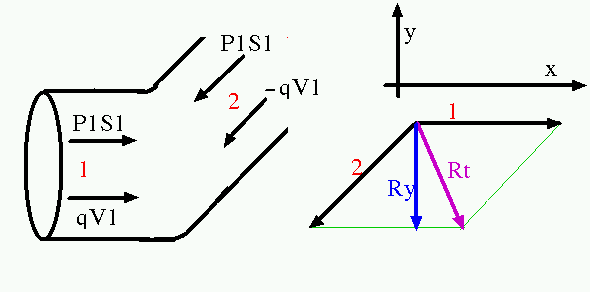
P1 = -245 Pa, S1 = 1,22 m², q = 30 Kg/s, V1 = 20 m/s.

L'effort dans la direction 1 vaut P1S1 + qV1.

L'effort dans la direction 2 a la même valeur absolue que pour 1, mais avec une orientation selon un angle de 135° par rapport à 1.

S'il existe, dans le système, une résultante non nulle qui puisse être assimilé à une portance, elle sera obligatoirement sur l'axe y (parce que vertical).

Dans le coude représenté ci-dessus, la résultante selon l'axe y (Ry) vaut:
-(P1S1 + qV1)multiplié par racine carrée de deux multiplié par 1/2 (le signe - parce que l'effort est vers le bas).

Cela donne: Ry = -(-245*1,22 + 30*20)*racine2/2 = -212,9098518 N.

Il y a deux coudes à 45° (bleus), la sommes des forces vers le bas produites dans ces deux coudes est de: -212,9098518*2 = -425,819703 N

2) Contraintes sur le coude à 90° (rouge):

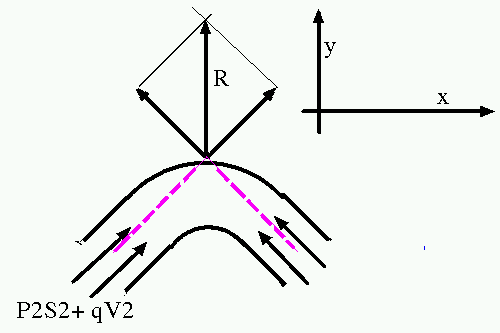
P2 = -980 Pa, S2 = 0.61 m², q = 30 Kg/s, V2 = 40 m/s.

Les deux composantes se croisent à 90°, la résultante vaut donc:
R = (P2S2 + qV2)multiplié par racine carrée de 2
R = (-980*0,61 + 30*40)*racine2 = 851,6394073 N

Peut-on faire l'additions des forces vers le haut et vers le bas tout de suite?

Non, car ce serait oublier que le système ne se compose pas exclusivement d'un coude étroit à 90° et de deux coudes larges à 45°, mais qu'il comporte aussi un convergent et un divergent dont, nous allons le voir, l'effet n'est pas nul, mais même compense exactement la différence entre les forces produites dans les coudes.

Contrairement à ce que l'on pourrait croire, les forces dans le convergent et le divergent ne s'annulent pas mutuellement par symétrie dans ce cas ci.

Pour que deux forces s'annulent mutuellement, il est absolument nécessaire qu'elles agissent suivant le même axe, mais en sens contraire, comme sur le dessin ci dessous:

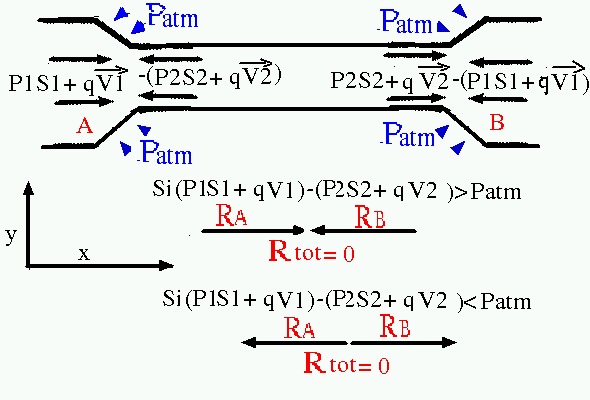
Le convergent et le divergent sont placés aux extrémités d'un tuyau droit, les forces éxercées dans l'un et l'autre sont donc toujours sur le même axe, et puisque par symétrie leur sens sont opposés, elles se contrarient mutuellement.

En d'autre termes, soit les forces se dirigent l'une vers l'autre (pour se contrarier mutuellement), soit elles s'écartent l'une de l'autre (toujours pour se contrarier).

Dans le système de tuyaux coudés dont nous calculons la résultante, les sections convergentes et divergentes ne sont pas placées aux extémités d'une jonction droite, mais plutôt d'un coude à 90° formant le sommet du système.

Dans ce cas, la résultante sera non nulle, verticale de bas en haut, si les forces sont dirigées l'une vers l'autre, et, toujours non nulle et verticale, mais orientée cette fois de haut en bas, si les forces s'écartent l'une de l'autre, comme nous le montre le dessin suivant: