Maintenant que l'on sait qu'il faut tenir compte des sections convergentes et divergentes, calculons y les forces et la résultante.

Il y a donc deux possibilités: soit les forces se dirigent l'une vers l'autre, et on obtient une résultante orientée vers le haut comme ci dessous,

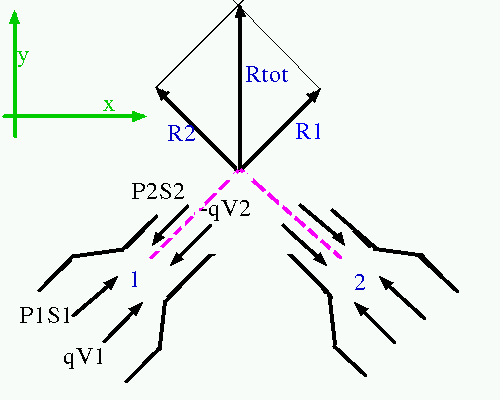
soit elles s'écartent l'une de l'autre, et on obtient une résultante orientée vers le bas, comme ci dessous:

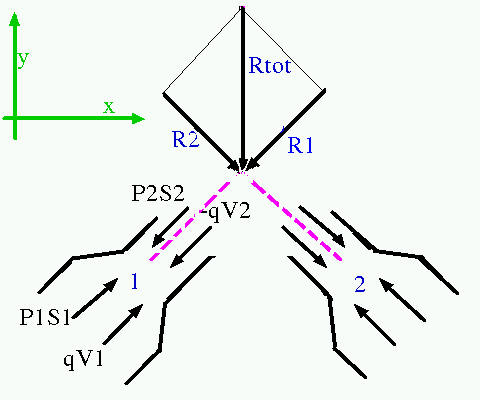
Rappel:
P1= -245 Pa, S1=1,22 m², q=30 Kg/s, V1=20 m/s, P2= -980 Pa, S2=0,61 m², V2=40 m/s.
Rappel: le signe * est le signe de multiplication.
R=((P1S1+qV1)-(P2S2+qV2))*racine2=((-245*1,22 + 30*20)-(-980*0.61 + 30*40))*racine2
R=((301,1)-(602,2))*racine2= -425,8197036 N

Le signe négatif indique une résultante orientée vers le bas, nous sommes donc dans le cas représenté par le dessin juste ci dessus, dont une copie simplifiée et réduite se trouve ci dessous:.

Maintenant que l'on a toutes les résultantes (coudes larges, coude étroit, convergent et divergent), faisons le total.

La résultante totale des deux coudes larges (bleus): -425,8197 N
La résultante totale du convergent et du divergent: -425,8197N
La résultante des forces dans le coude étroit (rouge): 851,6394
La résultante totale des forces dans tout le système:
851,6394 - 425,8197 - 425,8197 = 0 N!!!!

Avec une pression totale interne plus importante, par exemple: 101.000 Pa, on aurait:

P1= pression totale moins pression dynamique moins pression atmosphérique.
P1=(Pt - 1/2 rho (V1)²) - Patm = 101.000 - 1/2*1,225*(20)² - 100.000 = 755 Pa
P2=(Pt - 1/2 rho (V2)²) -Patm = 101.000 - 1/2*1,225*(40)² - 100.000 = 20Pa

Donc, cette fois, P1=755 Pa et P2=20 Pa, tandis que S1(1,22 m), S2(0,61 m), q(30Kg/s), V1(20m/s), V2(40m/s) restent inchangés.

Effort vertical dans un coude large à 45° (bleu): - (P1S1+qV1)*racine2 sur 2
Ry= - (755*1,22 + 30*20)*racine2 sur 2
Ry= -1521,1*racine2 sur2= -1075,580125 N
Il y a deux coudes larges donc: Ry tot= -1075,580125*2= -2151,16025 N

Effort vertical dans le coude étroit à 90° (rouge):
Ry=(P2S2 + qV2)*racine2 = (20*0,61 + 30*40)*racine2= 1212,2*racine2= 1714,30968 N

Effort vertical dans le convergent et le divergent:
Ry=((P1S1 + qV1) - (P2S2 + qV2))*racine2
Ry=((755*1,22 + 30*20) - (20*0.61 + 30*40))*racine2
Ry=(1521,1 - 1212,2)*racine2 = 436,8505694 N

Remarquez qu'avec une pression totale intérieure plus grande, la résultante des forces dans le convergent et le divergent est orientée, cette fois, vers le haut, on est donc dans le cas représenté par le premier dessin en haut de la page, et dont une copie simplifiée et réduite se trouve ci dessous.

Résultante totale du système: 1714,31 + 436, 85 - 2151,16 = 0 N!

D'une manière générale, et sans qu'il soit nécessaire de faire appel à des chiffres:
La résultante totale des deux coudes larges à 45° vaut: -(P1S1 + qV1)*racine2
Celle du convergent et du divergent vaut:((P1S1+qV1)-(P2S2+qV2))*racine2
Celle du coude étroit à 90° vaut: (P2S2 + qV2)*racine2.
Le total général vaut donc: - (p1S1 + qV1)*racine2 + (P1S1 + qV1)*racine2 - (P2S2 + qV2)*racine2 + (P2S2 + qV2)*racine2 = 0

On peut simplifier le système en le considérant comme une succession de:

1. Un coude à 45° dont la section de sortie est deux fois plus petite que la section d'entrée.
2. Un coude à 90° ayant partout la même section, c'est à dire celle de la sortie du premier coude. Ce coude à 90°formant le sommet du système.
3. Un nouveau coude à 45°, réplique du premier, pour retrouver une section de sortie du système égale à la section d'entrée, c'est à dire large.

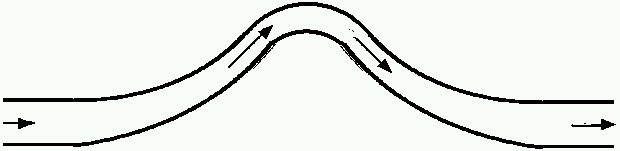
1)Coude à 45°

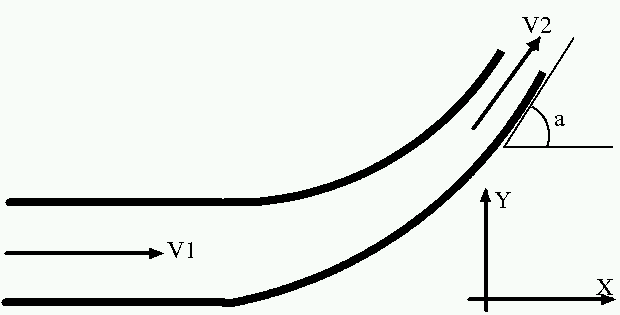
Efforts sur des coudes dont la section de sortie est différente de la section d'entrée, formule générale:
Fx=P1S1 - P2S2*Cosa + q*(V1 - V2 Cosa)
Fy= -(qV2 + P2S2)*Sina

Puisque seules les forces verticales comptent dans le cadre de la vérification de l'éxistence éventuelle d'une "portance", et que de toutes manière les forces horizontales (Fx) s'annulent mutuellement entre les deux coudes à 45° (elles sont sur le même axe (x), et sont orientées l'une vers l'autre), nous ne nous occuperons que de la composante verticale, donc Fy.

Il y a deux coudes, donc la résultante totale des deux coudes est:
Ry= -2*(qV2 + P2S2)*Sina.
a = 45°, donc Sina = racine carrée de 2 sur 2. La résultante Ry devient:
Ry= -2*(qV2 + P2S2)*racine2 /2
Ry= -(qV2 + P2S2)*racine2

Efforts sur le coude à 90°, formule générale:
Fy= (P2S2 + qV2)*racine2

La résultante totale des forces sur les deux coudes à 45° à section de sortie étroite, et du coude à 90° étroit est de:
Rtot= Fy + Ry = ((P2S2 + qV2)*racine2) - ((qV2 + P2S2)*racine2)= 0

En le montrant dans un cadre général non chiffré, on prouve ainsi que la résultante totale des forces dans ce genre de système est toujours nulle.

Tous ces petits calculs étaient uniquement destinés à satisfaire ceux qui doutent de la validité des principes physiques, même élémentaire.
Personellement, je n'ai pas besoin de me casser la tête à faire des calculs compliqués sur des systèmes compliqués, il m'a suffit de voir que le flux qui sort d'un système à exactement la même vitesse et la même orientation qu'à l'entrée pour en déduire qu'il n'y a pas eu, in fine, de modification de la quantité de mouvement, et sans modification de la quantité de mouvement, pas de force.

S'il existe, quelque part dans un système, une variation locale de la quantité de mouvement, et que cette variation n'est pas totalement compensée à un autre endroit du système, alors cela doit se traduire obligatoirement par une modification de la quantité de mouvement totale qui elle doit se traduire obligatoirement par une différence entre le flux entrant et le flux sortant.