Les fonctions dérivées, la suite...
Calcul
d'une dérivée.
Exemple chiffré:
Imaginons que nous ayons la fonction: f(x) = x², et que nous voulions trouver sa fonction dérivée.
Reprenons
l'expression du nombre dérivé: ce nombre est la limite, pour x1 tendant
infiniment vers x0, ou pour le dire autrement, pour x1-x0 tendant vers 0, de f(x1) - f(x0) sur x1 - x0.
On écrit: 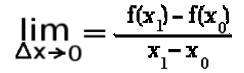 , soit limite pour delta x tendant vers 0 de f(x1) - f(x0) sur x1 - x0.
, soit limite pour delta x tendant vers 0 de f(x1) - f(x0) sur x1 - x0.
( delta x = différence des x, donc ici x1 - x0).
Ici, nous ne cherchons pas un nombre, fût-il dérivé, nous cherchons une fonction.
Nous ne donnerons donc aucune valeur numérique à X0 et X1, et procèderons comme suit:
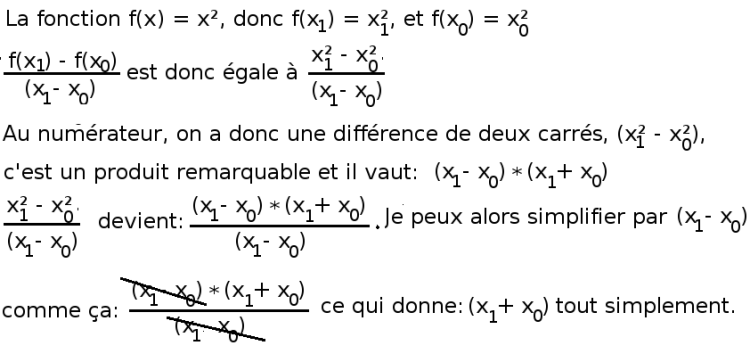
Maintenant (et seulement maintenant*)
je considère que puisque X1 tend infiniment vers X0, je peux dire (à la
limite) que X1 est égal à X0 et que je peux les désigner tous les deux
par X, tout simplement.
Donc: X1 + X0 = X + X = 2X.
Il vient: La dérivée de f(x) = x² est f'(x) = 2x.
*Parce
que: si j'avais posé X1 = X0 = X dès le début, je me serais retrouvé
avec un dénominateur (X1 - X0) nul! Et ça c'est pas bien, non, non,
non, c'est pas bien du tout, voilà!
On peut refaire le même
calcul avec f(x) = x³, on obtient, au numérateur une différence de deux
cube (X³1 - X³0), c'est encore un produit remarquable (X³1 - X³0) =
(X1 - X0)*(X²1 + (X1*X0) + X²0).
Après simplification par (X1 - X0), on a X²1 + (X1*X0) + X²0 au numérateur, et 1 au dénominateur.
On pose alors X1 = X0 =X et on a: X² + (X*X) + X² = X² + X² + X² = 3X².
La dérivée de f(x) = X³ est donc égale à f(x) = 3x².
Quelques dérivées usuelles:
Si
alors
f(x)= a (une
constante) f'(x)= o
f(x)= x
f'(x)=1
f(x)= ax
f'(x)= a
f(x)=x²
f'(x)=2x
f(x)=
xn
f'(x)= nxn-1
f(x)=
axn
f'(x)= anxn-1
f(x)=1/x
f'(x)= -1/x²
f(x)=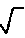 x
f'(x)= 1/2
x
f'(x)= 1/2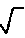 x (un divisé par deux
racine
carrée de x)
x (un divisé par deux
racine
carrée de x)
f(x)=Cosx
f'(x)=-Sinx
f(x)=Sinx
f'(x)= Cosx
f(x)=tgx
f'(x)=1/Cos²x ou
1+ tg²x
f(x)= lnx
f'(x)=1/x
f(x)=ex
f'(x)=ex
En désignant la fonction par f(x), ou g(x), ou h(x), et par leur dérivée respective par f'(x), g'(x), et h'(x):
Somme.
La
dérivée de (f(x)+g(x)) est f'(x)+g'(x)
(la
dérivée de la somme est égale à la somme des dérivées).
La
dérivée de (af(x)+bg(x)) est af'(x)+bg'(x) a et b
étant des constantes.
Produit.
La dérivée de (f(x)*g(x)) est f'(x)*g(x)+f(x)*g'(x) * étant le signe de multiplication.
Quotient.
La dérivée de f(x)/g(x) est f'(x)*g(x) - f(x)*g'(x) divisé par g²(x).
Inverse.
La dérivée de 1/f(x) est - f'(x)/f²(x)
Un exemple simple:
f(x)=12x³+3x²-8x+7
La
dérivée de la somme est égale à la somme des dérivées, donc:
f'(x)=(12x³)'+(3x²)'-(8x)'+(7)'
La
dérivée de axn = anxn-1 donc,
la dérivée 12x³= 12*3x², et la dérivée de 3x²=3*2x
La
dérivée ax=a, donc la dérivée de 8x=8,
et la dérivée d'une constante a=0, donc la
dérivée de 7=0.
f'(x)=(12*3x²)+(3*2x)-(8)+(0)
f'(x)=36x²+6x-8
Envie d'en savoir plus? envie d'un cours vraiment complet mais néanmoins clair et accessible sur les dérivées? clickez ici: http://freesciences.be/analyse.php.
En physique, on utilise pas ou peu la notation f'(x) pour désigner la dérivée, on préfère la notation de Leibnitz qui est df/dx, ou df(x)/dx, ou, puisque f(x)=y, on obtient dy/dx.
Il peut arriver parfois que l'on soit confronté à plusieurs variables, on dérive alors séparément pour chaque variable, ce sont les dérivées partielles.
Dans une dérivée partielle, la dérivation se fait par rapport à une seule variable, les autres variables étant alors considérées comme des constantes.
Souvenez-vous,
la notation de Leibnitz pour la dérivée est df/dx ou, plus simplement
dy/dx, pour la dérivée
partielle, on remplacera le d "normal" par le "d rond" comme ceci:
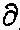
Exemple:
On
a une fonction à trois variables x y et z que l'on veut dériver.
La
fonction est f(x,y,z)= 4xy³ + 5y² + 3x²z
Si
on
dérive par rapport à x, on a: 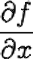 = 4y³
+ 6xz.
= 4y³
+ 6xz.
Si on dérive par rapport à y, on a: 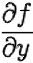 = 12xy²
+ 10 y.
= 12xy²
+ 10 y.
Si on dérive par rapport à z, on
a: 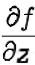 =3 x².
=3 x².
Encore
la même question (pas existentielle quand même): quelque chose de plus
complet sur les fonctions dérivées? je vous remet le même lien que
précédemment:
http://freesciences.be/analyse.php
Si l'on peut ainsi calculer la dérivée d'une fonction, peut on calculer, à partir d'une dérivée, quel est la fonction "d'origine" avant dérivation, et cela a-t-il un intérêt?
Oui, on peut, la fonction "d'origine" s'appelle alors la primitive, et l'intérêt de ce calcul est immense, comme nous allons le voir un peu plus loin.
Donnons
tout d"abord quelques
primitives usuelles:
Si:
alors sa primitive est:
f(x)=0
a (une
constante quelconque)
f(x)=a
ax
f(x)=x
1/2x²
f(x)=xa
,a étant différent de 1
xa+1divisé par (a+1)
f(x)=1/x
ln|x|
f(x)=1/x²
- 1/x
f(x)=1/xa
,a
étant différent de 1
- 1/(a-1)xa-1
f(x)=1/ 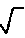 x
2
x
2 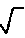 x
x
f(x)= lnx
x lnx - x
f(x)=Sinx
- Cosx
f(x)=Cosx
Sinx
f(x)=tgx
- ln
|Cosx|
f(x)=1+tg²x
ou 1/Cos²x
tgx
f(x)=ex
ex
Lorsque
l'on dérive une fonction de type: NIMPORTE QUOI + une constante,
cette dernière disparaît puisque la dérivée d'une constante est nulle.
On obtient donc la même
dérivée quelque soit la valeur de la constante.
Exemple:
La
dérivée de f(x)= 12x³+3x²-8x+7 est
égale à 36x²+6x-8.
La dérivée de
f(x)=12x³+3x²-8x-42
est aussi égale à 36x²+6x-8.
La dérivée
de f(x)=12x³+3x²-8x est elle aussi égale à
36x²+6x-8.
En sens inverse, lorsque l'on calcule
la primitive de la fonction f(x)=36x²+6x-8, que
doit on choisir?
12x³+3x²-8x, 12x³+3x²-8x+7,
12x³+3x²-8x-42, ou avec encore une autre constante?
Comme
n'importe quelle constante est valable, on dira simplement que la
primitive n'est définie qu"à une constante près que l'on rajoutera
systématiquement sous la forme d'un +c
(ou +k).
Exemples:
La primitive de
f'(x)=36x²+6x-8 est égale à f(x)12x³+3x²-8x+c.
La
primitive de f'(x)=1/x² est égale à
f(x)= -1/x+c.
A
la page précédente, pour faire comprendre l'intérêt du calcul de la
dérivée, on prenait l'exemple de l'accélération qui est la dérivée de
la vitesse par rapport au temps (a=dv/dt).
La vitesse est elle
même la dérivée de la distance (x) par rapport au temps (v=dx/dt).
Le premier intérêt du calcul de la primitive d'une fonction est donc le même que pour la dérivée mais en sens inverse: retrouver, par exemple, la fonction donnant la vitesse à partir de la fonction donnant l'accélération, ou celle donnant la distance parcourue à partir de la vitesse etc.....
Mais il y a un autre intérêt, le voici:
Calculer la surface d'un carré (un côté au carré), d'un rectangle (longueur fois largeur),ou d'un triangle (base fois hauteur sur deux) est extrêmement simple.
Calculer la surface d'un cercle (Pi*R²) ou d'une ellipse (Pi fois grand axe fois petit axe) n'est pas tellement plus compliqué.
Mais comment calculer la surface de ceci?

On pourrait par exemple estimer approximativement sa surface en la découpant en une série de rectangles, comme ceci:
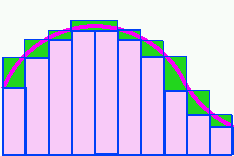
puis calculer la surface de chaque rectangle (facile) et additionner (encore facile).
Pour une approximation la plus juste possible, on peut même faire l'addition de tous les rectangles roses et y ajouter la moitié de la surface des rectangles verts, mais ce n'est encore qu'une approximation, pas la surface exacte.
Pour se rapprocher encore plus de la valeur exacte, on peut diviser la surface en rectangles plus petits et plus nombreux qui "colleront" mieux à la courbe.
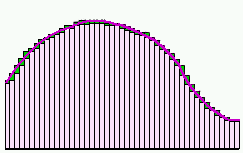
Si l'on pousse le raisonnement jusqu'au bout (à la limite), si l'on peut utiliser des rectangles dont la largeur tend vers 0, si l'on peut faire une somme (tendant alors vers l'infini) de ces rectangles, tous infiniments petits, la réponse sera EXACTEMENT égale à la surface réelle.
Si maintenant, nous reprenons la même forme dont on veut calculer la surface, et qu'on la place dans un repère orthonormé (avec axes X et Y).
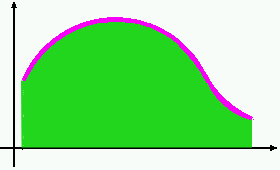
On peut la découper pareillement en une série de rectangles dont la largeur sera une différence d'abscisses et sera désignée par dx et la hauteur sera la projection du sommet du rectangle sur y et sera donc désignée par f(x).
Sur le dessin ci dessous, la largeur du rectangle de gauche est dx, mais quelle hauteur choisir, f(x1) ou f(x2)? Avec f(x1) la surface est trop grande, avec f(x2), elle est trop petite.
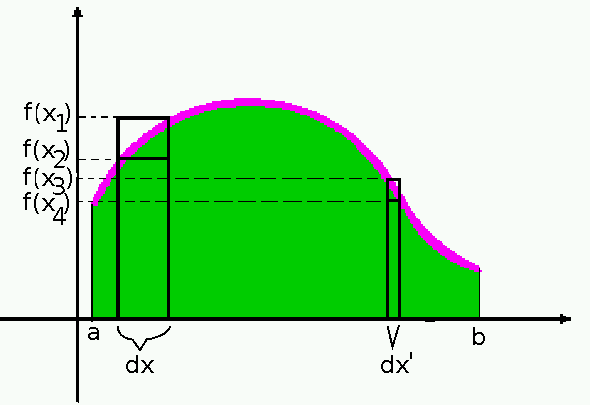
En prenant des rectangles plus étroits, donc des dx plus petits (ex: rectangle de droite de largeur dx'), il y a bien moins de soucis à se faire quant au choix de la hauteur. Le rectangle de droite étant beaucoup plus étroit (dx' <<<< dx), la différence de hauteur entre f(x3) et f(x4) est aussi plus faible.
En poussant ce raisonnement au maximum, donc à la limite, pour un dx infiniment petit, les deux "hauteurs possibles" peuvent être considérées comme confondues en une seule que l'on désignera par f(x) tout simplement.
La surface d'un tel "rectangle élémentaire" sera donc: la hauteur (unique) fois la largeur, c'est à dire: f(x)*dx.
En additionnant ainsi tous ces rectangles infiniment petits qui "collent" parfaitement à la courbe, on obtient EXACTEMENT la vraie valeur de la surface.
Puisque ces rectangles sont infiniment petits, il en faudra un nombre tendant vers l'infini pour "remplir" toute la surface à calculer.
La
surface à calculer est donc égale à la somme (tendant vers l'infini)
des f(x).dx
entre le point a et le point b, ou, pour le dire autrement: somme de a
à b des f(x).dx que l'on écrira: 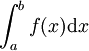 , le signe:
, le signe: 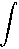 n'étant, en fait qu'un grand S allongé pour rappeler l'idée de somme,
alors que l'expression se dit: INTÉGRALE de a à b de f(x) dx.
n'étant, en fait qu'un grand S allongé pour rappeler l'idée de somme,
alors que l'expression se dit: INTÉGRALE de a à b de f(x) dx.
Le
rapport avec les primitives?
Le fait que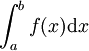 est
égale à F(b) - F(a), F(x) étant une primitive de f(x)
est
égale à F(b) - F(a), F(x) étant une primitive de f(x)
ou
pour le dire en français: intégrale de a à b de f(x).dx est égale à
l'image de b par la fonction primitive moins l'image de a par cette
même fonction primitive.
Le terme d'intégrale (tout court) ou d'intégrale INDÉFINIE est souvent utilisé pour désigner la primitive.
Le calcul intégral permet donc de calculer l'aire de toute surface du moment que l'équation de la courbe délimitant cette surface est connue.
Par extension, le même principe permet de calculer des volumes, et d'une manière générale le calcul intégral est utilisé chaque fois que ce que l'on cherche à calculer peut être considéré comme le résultat de la somme d'un nombre tendant vers l'infini de petites contributions élémentaires.


