LES FONCTIONS DERIVEES
Ceci n'est pas un cours sur les fonctions dérivées, il s'agit simplement de faire comprendre, à ceux qui n'en ont pas ou peu entendu parler, ce qu'elles représentent, et pourquoi elles sont si importantes en physique.
Si, par contre, vous recherchez quelque chose de plus évolué sur les fonctions dérivées il y a ce que vous cherchez ici: http://freesciences.be/analyse.php
Autre possibilité, si vous n'êtes pas sûr du niveau que vous recherchez, lisez ce qui suit et, si ça vous tente d'en savoir plus, clickez sur le lien donné qui vous sera de nouveau proposé à la fin.
Disons d'abord ce qu'est une fonction toute simple.
A la télé, ou dans des revues, on peut voir des graphiques de ce genre, représentant, par exemple, l'évolution du prix du pétrole sur un certain nombre de mois, ou l'évolution de la température d'un malade sur quelques jours. On pourra dire que ce graphique représente l'évolution du prix du pétrole ou de la température d'un malade en FONCTION du temps.
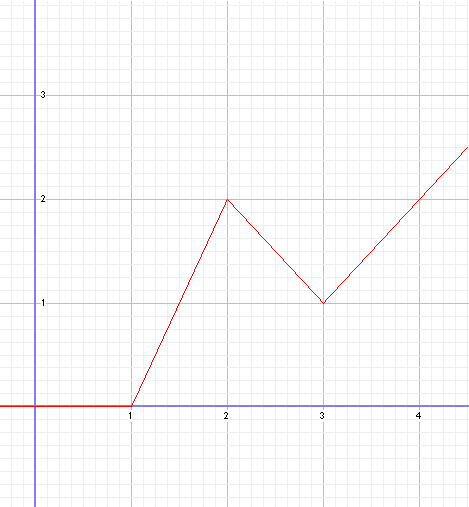
Voici la représentation graphique d'une autre fonction.
Elle peut aussi bien représenter l'évolution d'une vitesse par rapport au temps que la hauteur d'une dune par rapport à sa distance de la mer.
Si seul l'étude du graphique compte, inutile de spécifier ce qu'il représente (vitesse, hauteur, prix etc..). Dès lors, et pour être plus général, l'axe horizontal s'appellera: axe des X ou abscisse; et l'axe vertical s'appellera: axe des Y ou ordonnée.
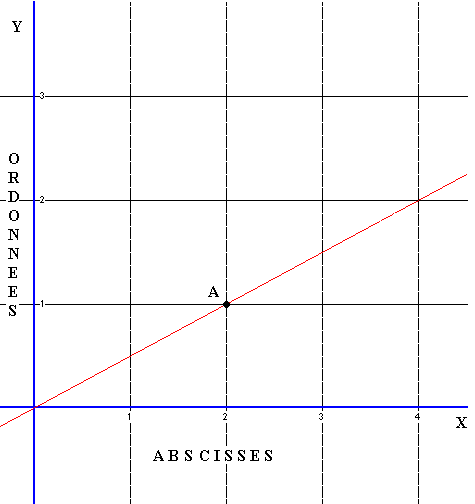
Chaque point du graphique sera désigné par 2 nombres correspondant à leur projection respectivement sur l'axe des X et sur l'axe des Y. Par exemple, le point A a pour abscisse 2 et pour ordonnée 1; ses coordonnées sont donc: (2 , 1).
Si l'on se déplace de gauche à droite, on voit que la droite représentant la fonction monte d'UNE case pour un déplacement latéral de DEUX cases. On dira que le COEFFICIENT DIRECTEUR de la droite est de un sur deux, donc: 1/2.
Le coéfficient directeur nous renseigne donc sur une propriété de la fonction: la croissance.
Pour un coéfficient directeur nul, la droite est horizontale; S'il est négatif, la droite "descend". S'il est positif, la droite "monte".
Le coéfficient directeur peut aider aussi à trouver l'équation qui caractérise la fonction. Ici, le coéfficient directeur est de 1/2, donc l'ordonnée est toujours moitié moins grande que l'abcisse.
L'ordonnée, c'est Y, donc: y= 0.5x sera l'équation de cette droite. Y est l'image de x par la fonction f , on dit y= f(x) (y= f de x).
Voici (en dessous) un autre graphique, comportant deux fonctions cette fois.
L'une est une droite horizontale (ordonnée: 2). Dans ce cas, quelque soit la valeur de x (abscisse), y (l'ordonnée) vaut toujours 2. Son coéficient directeur est 0 (pas de pente) et son équation est simplissime, c'est: y=2.
L'autre fonction est une droite très "pentue". Si je dessine une
sorte de marche d'escalier pour mesurer les déplacements latéraux et
verticaux, je constate un déplacement vertical 2 fois plus important
que le déplacement horizontale (on monte de 2 pour un déplacement de
un). Son coéficient directeur est donc 2.
Elle ne passe pas par le point (0 , 0) ( croisement des deux axes),
mais par le point (0 , 1). A l'origine (0 en abscisse), elle a déja
une "avance" de 1 en ordonnée.
Dans son équation, on aura donc: 2x puisqu'elle "monte" 2 fois plus vite que son déplacement selon l'axe des x ET on rajoutera +1 pour son avance de 1 en ordonnée à l'origine.
La fonction f(x) s'écrira alors: y= 2x + 1.
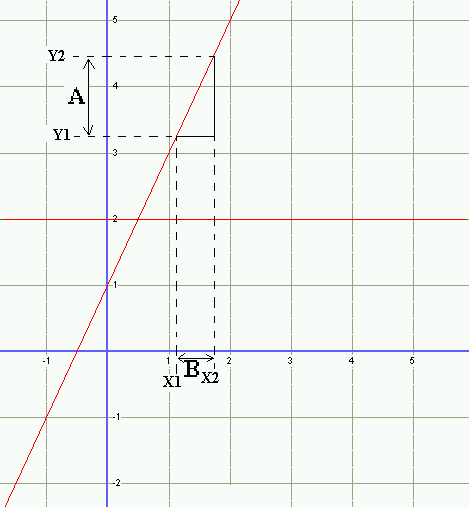
La hauteur de la "marche" correspond à la différence entre les deux
points de projection sur l'axe des ordonnées.
On peut écrire: A= Y2 - Y1.
La profondeur de la "marche" correspond à la différence entre les
deux points de projection sur l'axe des abscisses.
On peut écrire: B= X2 - X1.
Le coéfficient directeur étant le rapport entre la hauteur de la
marche et sa profondeur, il est donc égal à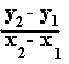 
Voici toute une série de fonctions dont le coéfficient directeur va de -1 à + 4.
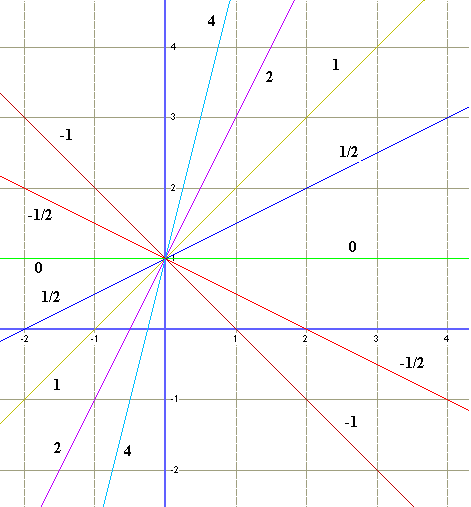
Les coéfficients directeurs sont inscrits deux fois sur chaque droite.
Calculer la pente d'une fonction, c'est donc calculer son évolution, de cette façon, c'est facile, puisque ce sont des droites. Mais comment faire si la fonction n'est pas une droite mais une courbe, comme celles-ci:
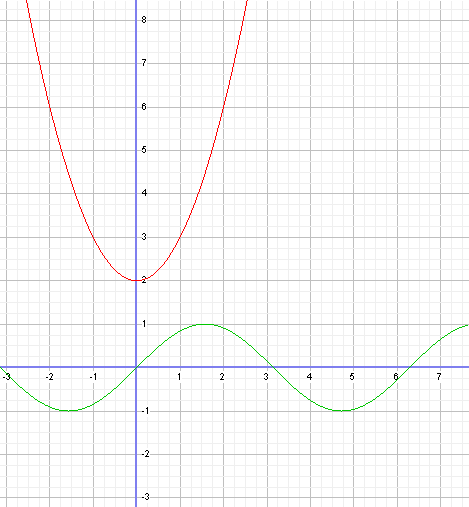
La première est une parabole (en rouge), la deuxième est une
sinusoïde (en vert).
Puisque ce sont des courbes, la pente change continuellement, le
coéfficient directeur aussi.
Lorsque le graphe de la fonction est une droite, la pente est la même, qu'elle soit calculée sur un grand ou un petit écart.
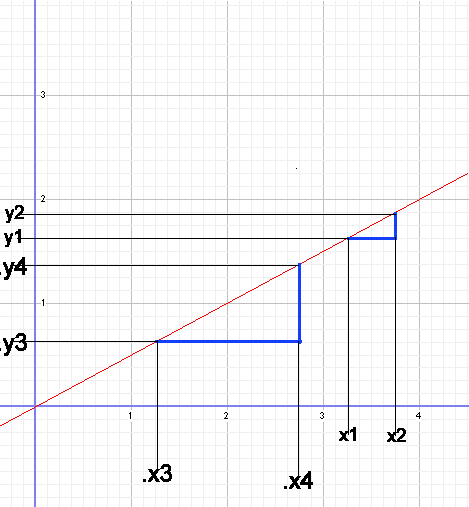
Le coéfficient directeur est tout aussi bien égal 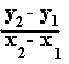à qu'à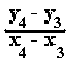 
puisque: =
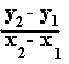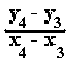
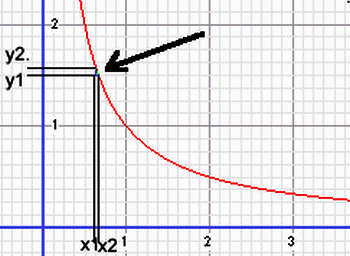
Sur une courbe, le calcul sur un grand écart est beaucoup moins fiable que sur un petit, il peut même être fort différent. D'ailleur, la méthode utilisée jusqu'ici, ne donnera pas le coéfficient directeur de la courbe (impossible, ça change tout le temps), mais le coéfficient directeur du segment joignant les deux extrémités de la "marche".
Ce qui correspond à la corde de l'arc choisi (ligne verte)
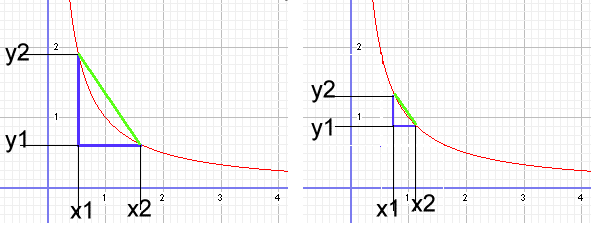
Remarquez, sur le dessin de droite, que plus le segment de courbe (l'arc) est choisi petit (en choisissant un écart entre X1 et X2 lui aussi petit, et donc une différence X2 - X1 petite), plus le segment de courbe (l'arc) est choisi petit donc, plus la différence entre l'arc et la courbe est faible.
Dans ce cas, le coéfficient directeur de la corde (en vert) donne déja une meilleur idée de la variation de la courbe.
Toutefois, transformer une courbe en une suite de petits segments droits est long à réaliser et encore trop imprécis.
Même des segments super petits comme sur le dessin de droite ne donnent pas encore la précision parfaite souhaitée.
L' idéal n'est donc pas de calculer le coéfficient directeur d'une
corde, même très petite, mais c'est de pouvoir le calculer en
un seul point.
Réduisons donc notre écart d'abscisse (donc X2 - X1) à presque rien pour pouvoir travailler sur une portion de courbe quasiment réduite à un point.
Pour cela, il faut choisir des abcisses X1 et X2 infiniment proches, tellement proches qu'elles sont comme confondues. Ou, pour le dire autrement, il faut pousser la réduction de l'écart entre X1 et X2 à la limite...
On obtiendra, alors le coéfficient directeur de la TANGENTE en ce point.
On ne peut pas faire mieux, la tangente ne touchant la courbe qu'en UN point. Ce coéfficient de la tangente est aussi un rapport entre deux différences*, mais sur un interval infiniment petit.
(*) Toujours comme pour le coefficient directeur d'une droite, donc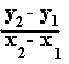
On appellera NOMBRE DÉRIVÉ le coéficient directeur de la tangente en un point de la courbe.
Rappelez vous maintenant ce qui a été dit au début, à savoir: y est l'image de x par la fonction f , on dit y= f(x).
Du coup, on peut remplacer "y" par "f(x)
Et on aura alors l'expression purement mathématique suivante:
pour une fonction Y= f(x), la limite pour X1 tendant vers X0 de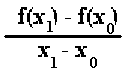 
s'appelle le nombre dérivé.
On a remplacé X1 par X0 et X2 par X1, mais ça ne change rien à la logique. Rappelez vous plus haut, on avait aussi des X3 et X4, parce que l'explication demandait plus d'interval, c'est tout. Les indices (0, 1, 2, 3, 4) ne sont là que pour différencier les x (ou les y) rien de plus.
On peut dire aussi que le nombre dérivé est la valeur de y1-y0/x1-x0 quand x1 s'est rapproché le plus possible du plus possible du plus possible de x0 (la limite), ou si vous préférez lorsque l'écart entre x1 et x0 est devenu infiniment petit.
Maintenant que nous savons ce qu'est un nombre dérivé, disons que la fonction dérivée est celle qui réunit tous les coéfficients directeurs des tangentes.
Comment?
en faisant correspondre à chaque valeur de x, le coéfficient angulaire
de la tangente à la courbe pour cette même valeur de x.
Remarquez, si on calcule la dérivée d'une fonction dont le graphe est
une droite, on trouve, tout simplement son coéficient directeur; comme
ceci:
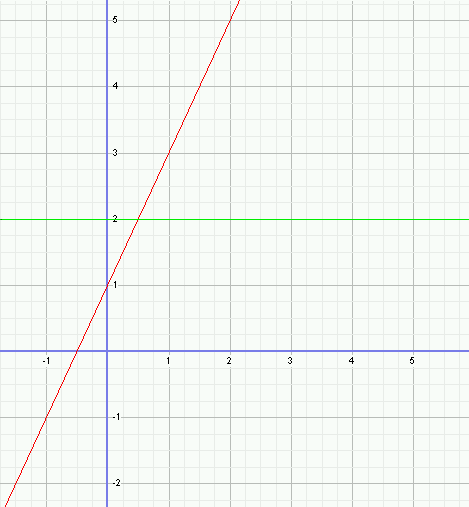
La fonction f(x) c'est: y= 2x + 1 (droite rouge); la fonction dérivée f'(x) est: y= 2 (droite verte).
La fonction dérivée nous renseigne sur la variabilité de la fonction de départ. Ici, y= 2 nous dit que le coéfficient directeur de la droite rouge est TOUJOURS 2 car sur la droite y= 2, quelque soit x, y vaut TOUJOURS 2.
Si la fonction de départ est une courbe (une parabole par exemple), le coéfficient directeur change constamment, donc, la fonction dérivée n'est pas horizontale (y n'est pas inchangé quelque soit x).
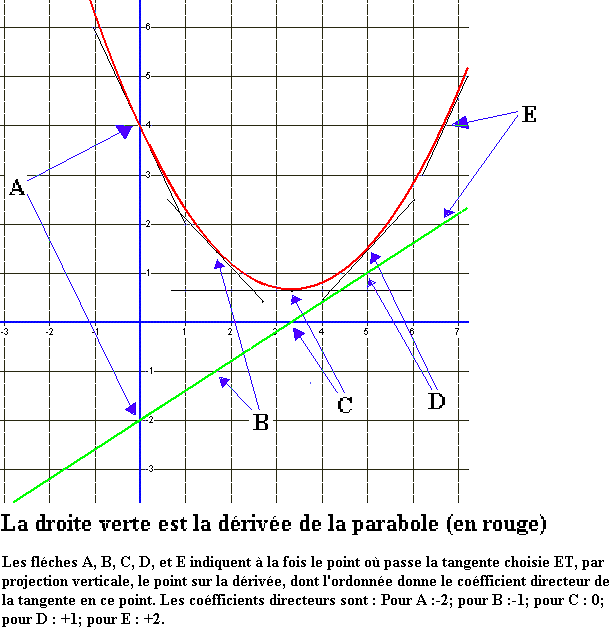
Pour bien se représenter le rapport entre les coéfficients directeurs des tangentes et la fonction dérivée, je les ai fait correspondre ici:
Voici un autre exemple:
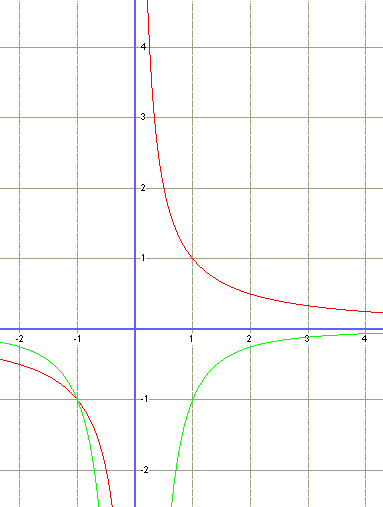
La fonction 1/x en rouge et sa dérivée en vert. cette fois la dérivée est une courbe.
Pareil ici avec la fonction: y= x³ (en rouge), et sa dérivée (en vert).
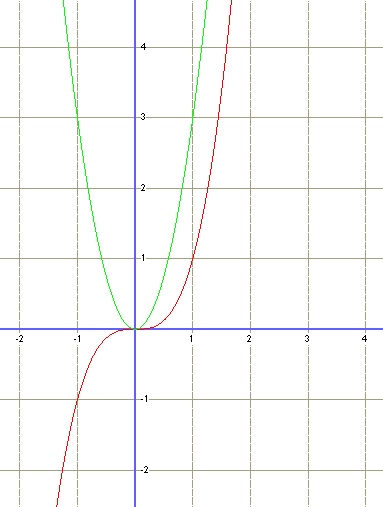
La dérivée est donc "l'image" de la variabilité d'une fonction, ou pour être plus précis, la dérivée donne le TAUX DE VARIATION de la fonction .
Le "taux de variation" de la vitesse c'est l'accélération (ou la décélération, mais ce n'est qu'une accélération négative). Il est donc normal, qu'en physique, l'accélération soit représentée et calculée comme la dérivée de la vitesse par rapport au temps (la vitesse se met en ordonnée, et le temps en abscisse).
On écrit: A= dv/dt, ce qui signifie que A= la dérivée de la vitesse par rapport au temps, mais on peut dire aussi pour simplifier: A= la VARIATION de la vitesse sur la VARIATION du temps, considérant ainsi le petit d comme signifiant: "variation de", juste pour la simplicité.
A=dv/dt n'est qu'un exemple d'application physique de la dérivée, vous pouvez en trouver plein d'autres.
La dérivée permet de connaitre aussi les fluctuations de la fonction (croissance, décroissance, etc...). En particulier, si la dérivée est nulle en un point, c'est que la tangente en ce point est horizontale (coéfficient directeur 0), donc, que la fonction ne croit ni ne décroit (à un maximum ou à un minimum).
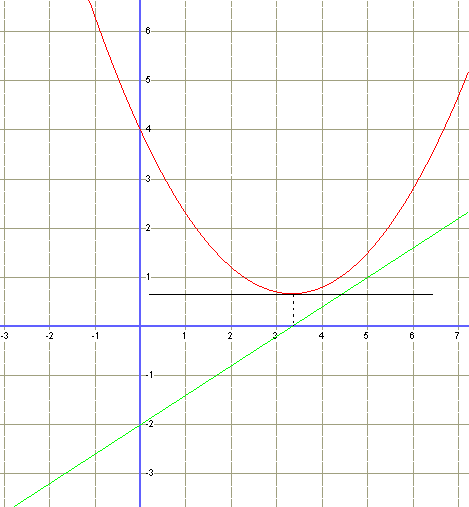
Ici, la parabole (en rouge) passe par un minimum, la tangente (en noir) est horizontale, et le coéfficient angulaire est nul (la dérivée (en vert) traverse l'axe des x, là où l'ordonnée est nulle.
En physique, pouvoir étudier en détail des phénomènes évolutifs (vitesse, accélération, courant etc...) est très important, et pour cela les dérivées sont incontournables..
