QUELQUES EXEMPLES.

Si l'on cherche à mesurer la quantité d'électricité qui est passée dans un fil ou dans un appareil entre deux instants donnés, on fait, comme pour un liquide dans une canalisation, le produit du débit par le temps.

Exemple pour un liquide: si le débit est de 15 litres par seconde et le temps de 30 secondes, on obtient au bout des 30 secondes d'écoulement une quantité totale de liquide valant: 15 fois 30 = 450 litres.

Exemple pour de l'électricité: si l'intensité (équivalent du débit) est de 15 ampères (donc 15 coulombs par seconde) et le temps de 30 secondes, on obtient au bout des 30 secondes de passage de courant une charge totale de 15 fois 30 = 450 coulombs.

Je peux représenter n'importe lequel de ces deux exemples sur le même graphique: celui ci:

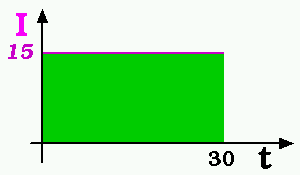
Le produit de 15 par 30, qui représente aussi bien la quantité d'électricité que la quantité de liquide des exemples ci dessus, correspond, sur ce graphique, à la surface colorée en vert, je peux donc trouver cette quantité en calculant la surface du rectangle qui vaut 15 fois 30 = 450; c'est bien la réponse attendue.

Enfin, je peux aussi me dire que s'il y a surface, il y a possibilité d'utiliser le calcul intégral.
Dans ce cas, on peut dire que la ligne mauve qui, sur le dessin, donne la limite supérieure du rectangle vert est un segment de la droite d'équation y=15,
la primitive sera donc: F(x)=15x, et l'intégrale définie de 0 à 30 sera égale à: F(30)-F(0)=(15*30)-(0*30)=450.
On obtient encore la même (bonne) réponse.

Si le débit de liquide ou d'électricité commence à 15 litres par seconde (pour le liquide) ou 15 ampères (pour l'électricité) et diminue régulièrement pour devenir nul au bout de 30 secondes, on obtient ce graphique:

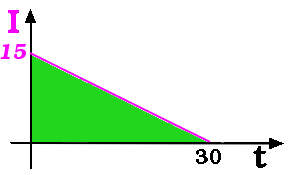
La quantité totale de liquide ou d'électricité au bout de 30 secondes est toujours représentée, sur le dessin, par une surface, mais cette fois il s'agit d'un triangle.

Pour résoudre ce problème, presqu'aussi simple que le précédent, on peut, par exemple, dire que puisque le débit passe de 15 à 0 par une diminution constante et régulière, cela signifie que le débit moyen est de:
(15+0)/2 = 15/2 = 7,5 (ampères ou litres par seconde peu importe).
Ensuite, il suffit de faire le produit du débit par le temps, et on obtient:
7,5 * 30 = 225 (coulombs ou litres suivant qu'il s'agisse d'éléctricité ou de liquide).

On peut aussi partir du dessin et constater que la surface représentant la quantité recherchée est un triangle.
On sait que l'aire d'un triangle vaut: base fois hauteur divisé par deux, ce qui donne dans ce cas: (30 * 15) / 2 = 225 (on retrouve donc la même valeur).

Enfin, on peut aussi dire que la ligne mauve formant l'hypoténuse du triangle rectangle vert est un segment de la droite d'équation:
y = 15 - 1/2 x. La surface "sous la droite" entre l'origine (donc 0) et 30 vaut: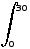
15 - 1/2x = F(30) - F(0)
La primitive: F(x)= 15x - x²/4
F(30) = 15*30 - 30²/4 = 450 - 900/4 = 450 - 225 = 225
F(0) = 15*0 - 0²/4 = 0
Donc F(30) - F(0) = 225 - 0 = 225
Ici aussi on retrouve la même valeur (heureusement!!)

Nous n'avons montré, juqu'ici que des cas extrêmement simples pour lesquels une multiplication suffit, mais ils montrent bien que certaines quantités physiques peuvent être représentées, sur un graphique, par une surface et calculées en mesurant cette même surface, or qui dit surface dit possibilité d'utiliser le calcul intégral.

S'il n'est absolument pas nécessaire d'utiliser le calcul intégral pour les exemples précédents du fait de leur extrême simplicité, il n'en sera pas toujours de même.

Reprenons notre exemple de la quantité d'électricité, mais calculons la cette fois dans le cadre de la charge d'un condensateur.

Pour ceux qui ne savent pas ce qu'est un condensateur, on en parle ici.

Les courbes représentant l'évolution de la tension (courbe bleue: U) et de l'intensité électrique (courbe rouge: I) lors de la charge d'un condensateur ressemblent à ceci:

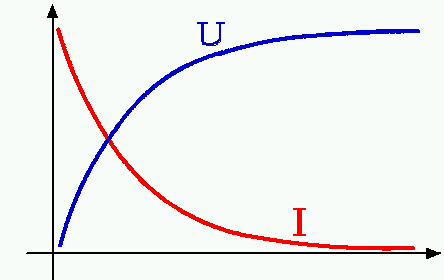
La courbe rouge représente le "débit de charge" (ou intensité ou courant), et si nous voulons connaître la quantité totale de charges "recue" par le condensateur, il faudra calculer la surface "sous" la courbe.

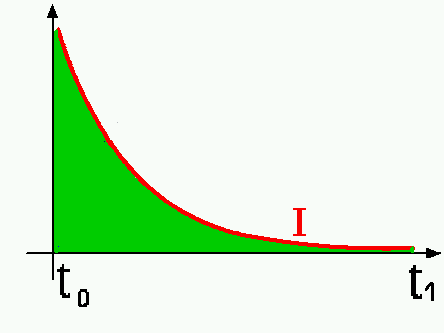
On s'aperçoit tout de suite que le calcul précis d'une telle surface ne peut se faire par une simple multiplication, il faut passer par le calcul intégral.
L'intensité, c'est un débit de charge, c'est donc une variation de la charge par rapport au temps.
Une variation s'exprime par une dérivée, donc l'intensité I = dq/dt.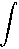
I dt = 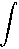dq/dt * dt = Q
La capacité (C) d'un condensateur c'est la quantité de charges (Q) qu'il peut stocker par unité de tension (U), donc C = Q/U et Q = C*U.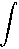
dq/dt * dt = 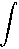C*du/dt * dt = C * 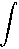du/dt * dt = C*U.
Si l'on connait l'équation de la courbe I ou celle de la courbe U et la capacité du condensateur (C), on peut trouver la charge à n'importe quel moment, en calculant l'intégrale définie de t0 à t1.

Un autre exemple: l'énergie contenue dans un condensateur.

Pour trouver l'énergie, on peut faire le produit de la puissance par le temps (E = P*t), la puissance elle-même pouvant être trouvée en faisant le produit de la tension par l'intensité (P = U*I).

Voici la courbe de puissance d'un condensateur:

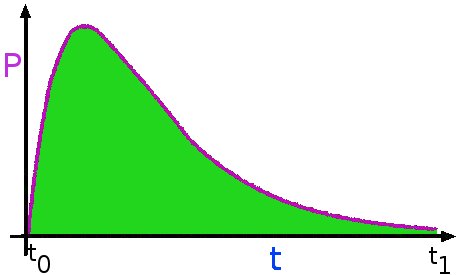
Etant donné la forme de la courbe, on voit tout de suite qu'il est impossible de se contenter de faire P fois t pour obtenir la surface verte délimitée par la courbe et les axes, pourtant c'est bien cette surface qui représente l'énergie que l'on veut mesurer. Une seule solution: le calcul intégral.

Je ne connais pas l'équation de la courbe de puissance, comment vais-je donc pouvoir en trouver l'intégrale?
En contournant le problème, en exprimant la puissance en fonction de la tension (U) et de l'intensité (I).
La puissance est le produit de la tension par le courant (l'intensité), donc:
p = u * i.

Ici, la tension, l'intensité et donc aussi la puissance varient en fonction du temps, ce sont donc des fonctions dont la variable est le temps.

On a vu plus haut que i = dq/dt (l'intensité est la variation de charge sur le temps, donc le débit), et que la capacité (C) d'un condensateur c'est la quantité de charges (Q) qu'il peut stocker par unité de tension (U), donc C = Q/U et donc: Q=C*U. On peut donc en déduire dq/dt = C*du/dt.
L'équation: i = dq/dt devient donc: i = C*du/dt.
L'équation: p = u * i devient p = u * C*du/dt, que l'on peut écrire: p = C*u*du/dt.
L'énergie est égale à: 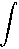p*dt donc à: 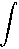C*u*du/dt * dt = C *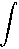u * du/dt * dt = C *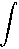u * du.

La primitive de u, c'est 1/2 u², donc C *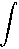u * du = C*1/2*u² ou 1/2*C*u².
L' énergie d'un condensateur vaut donc: E = 1/2 C u².

Pour terminer, s'il vous arrive de rencontrer des intégrales qui semblent s'être dupliquées, comme ceci: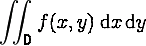
,
voir comme cela: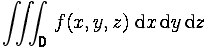
,
ou pire encore, il s'agit tout simplement d'intégrales multiples, c'est à dire d'intégrales de fonctions à plusieurs variables.

Elles se calculent en intégrant par rapport à une première variable, puis par rapport à une deuxième, et ainsi de suite autant de fois qu'il y a de variables.

De plus plus souvent, et par facilité, les intégrales multiples s'écrivent avec un seul signe intégral, le nombres de variables suffit à montrer le caractère multiple.

Si une intégrale simple représente la surface délimitée par la courbe de la fonction, l'axe des abscisses (x), et les droites aux deux bornes d'intégration, l'intégrale double représente le volume délimité par la surface (représentant la fonction à deux variables) et le domaine d'intégration D.

L'intégrale triple représente ce qu'on appelle un hypervolume (avec 4 dimensions spatiales) qu'on ne peut ni dessiner ni même vraiment se représenter, alors que dire des intégrales quadruples, quintuples, ou au delà.......