AccueilGallerieDefence daysLiens

LES FUSEES A ETAGES

Peut-on prévoir d'avance la vitesse finale d'une fusée en connaissant son poids au départ, la vitesse d'éjection de ses gaz, et la quantité de propergols qu'elle emporte ?

Oui, voici comment :

on connait la vitesse d'éjection de ses gaz (V_e), sa masse au départ (M₀), et sa masse en fin de fonctionnement des moteurs (M₀ moins la masse de propergol consommé).

Cette masse en fin de combustion c'est M₁. On place tout cela dans la formule inventée par Tsiolkowski (prononcez.... comme vous pouvez!).

Voici cette formule : V_f = 2.3* V_e* log.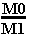

Avec V_f = vitesse finale, et V_e = vitesse d'éjection des gaz.

Remarquez que j'utilise le logarithme en base 10, plus familier à certain, mais le logarithme népérien marche aussi, et ça donne :

V_f = V_e* ln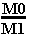.              ( attention, pour les non habitués, * signifie multiplié par).

Application : Soit une fusée de 500 tonnes contenant 450 tonnes de propergols, et 10 tonnes de charge utile (donc, 40 tonnes de structure), avec une vitesse d'éjection des gaz de 3000 m/s. Le tout ne formant qu'un seul étage. On aura, suivant la formule :

V_f = 2.3 * 3000 * log 500/50 = 6900 m/s

ou

V_f = 3000 * ln 500/50 = 6900 m/s

(calcul réalisé en négligeant l'attraction terrestre et la traînée aérodynamique, la V_f réelle serait donc plus basse*).

(*)En fait, pour l'influence de l'attraction terrestre, il "suffit" retrancher le produit de l'accélération de la pesanteur (G) par la durée de combustion (t),

soit:

V_f = V_e * ln Mo/M₁ - G * t,  ou V_f = 2,3 * V_e * log Mo/M₁ - G * t, pour la traînée aérodynamique c'est plus compliqué....

Etant donné que la vitesse de satellisation minimum est d'environ 8000 m/s, cette fusée serait incapable d'y parvenir.

Divisons la fusée en deux étages : 1 étage de 400 tonnes dont 30 tonnes de structure, et un étage de 100 tonnes dont 10 tonnes de structure et 10 tonnes de charge utile (le satellite).

Pour le premier étage, on a : V_f = 3000 * ln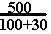 ou  V_f = 2.3 * 3000 * log.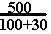

Avec : 500= masse totale de la fusée au décollage, 100+30 = masse de la fusée en fin de combustion du premier étage, c'est à dire, tout le deuxième étage et sa charge (100t), plus la stucture à vide du premier étage (30t).

Donc, V_f = 3000 * ln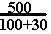 = 4036.5 m/s.    ou  V_f = 2.3 * 3000 * log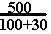 = 4036.5 m/s.

Pour le deuxième étage, on a :  V_f = 3000 * ln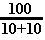 ou V_f = 2.3 * 3000 * log,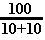

avec: 100 = masse totale du second étage, 10+10 = masse du second étage en fin de combustion, c'est à dire, la structure à vide du deuxième étage, plus le satellite.

V_f = 3000 * ln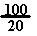 = 4923.1 m/s.  ou  V_f = 2.3 * 3000 * log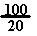 = 4923.1 m/s.

Puisque le deuxième étage démarre avec la vitesse initiale donnée par le premier étage, il faut additionner les vitesses acquises par chacun des 2 étages pour obtenir la vitesse finale atteinte pour le satellite.

Ce qui nous donne : 4036.5 + 4923.1 = 8959.6 m/s, la vitesse de satellisation est atteinte largement, mais on a toujours pas tenu compte de l'attraction terrestre.

Ce n'est pas grave, le seul but de ces calculs était de démontrer la supériorité du système à étage.

En fait, le secret de la fusée à étage est de s'allèger en larguant, somme toute, les réservoirs vides. Le fait que ces reservoirs vides soient accompagnés de moteurs fusées, n'est qu'un effet secondaire inévitable, qui oblige chaque étage à avoir ses propres moteurs. Voici une illustration assez claire, où l'on montre le premier étage fonctionnant jusqu'au bout de ses réservoirs :

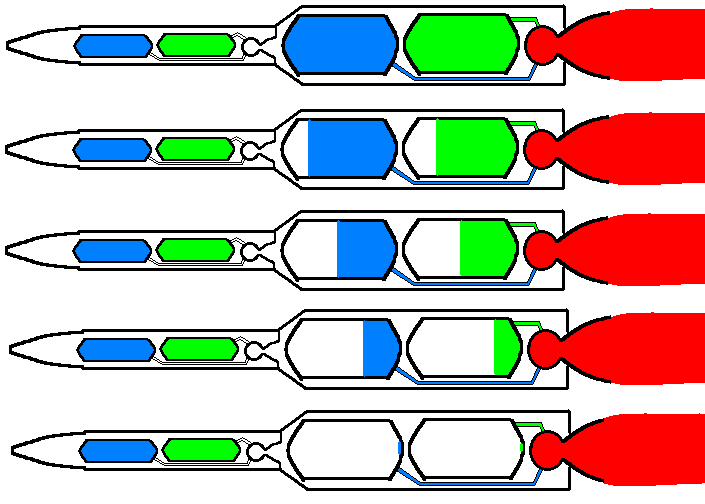
Ensuite, il y a séparation par explosion de boulons explosifs, et le deuxième étage prend la relève, sans avoir à supporter le poids, désormais inutile, du premier étage.

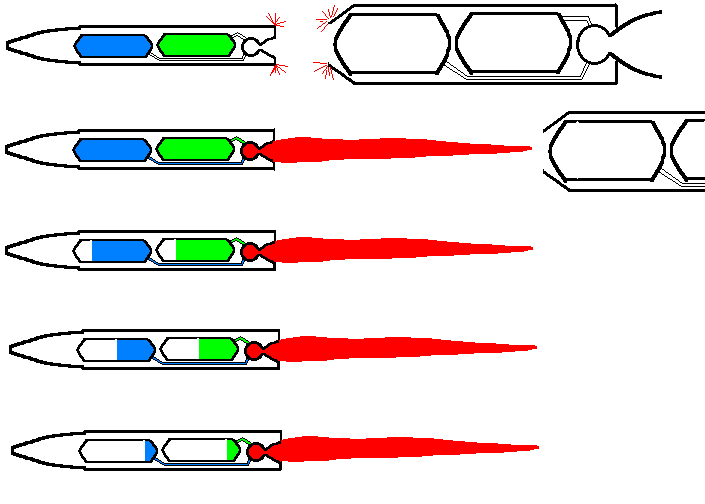
Enfin, arrivé à l'altitude, et la vitesse prévue, la coiffe du nez de la fusée s'ouvre, libérant le satellite.

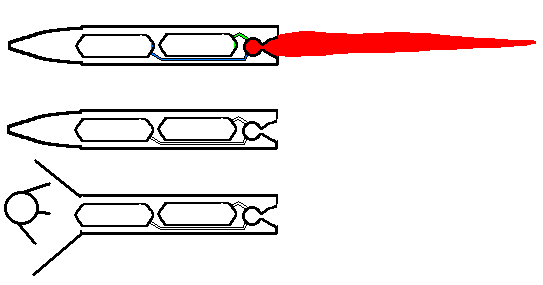
Ici, les moteurs ont fonctionnés jusqu'à épuisement des propergols; ce ne sera pas forcément toujours le cas, bien que la quantité de propergol embarquée soit bien calculée, les moteurs sont arrêtés dès que la vitesse et l'altitude recherchées sont atteintes, quelque soit la quantité de propergols restante (cette quantité n'est jamais très importante si les calculs ont été bien faits).

On a toujours pas répondu à la question de départ : Peut-on, oui ou non, satelliser, par moteur fusée auxilliaire, un avion hypersonique volant à 10000 km/h ?

Prenons un avion hypersonique de 200 tonnes en charge, capable de voler à 3400 m/s (12240km/h).

Pour être satellisé, il faut atteindre 8000 m/s.

Sa vitesse étant déja de 3400 m/s, il lui reste à acquérir une vitesse supplémentaire de 4600 m/s.

Il est équipé de moteurs à hydrogène et oxygène liquides lui permettant des vitesses d'éjection de 4000 m/s.

La formule devient : 4600 = 4000 * ln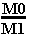   ou  4600 = 2.3 * 4000 * log.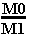

Donc:

                

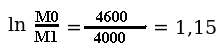
L’inverse du logarythme népérien de 1,15, c’est (environ) 3,16

ou, pour le dire autrement: e^1,15 = 3,16

Et donc, 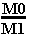= 3.16.          

ou  log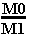 = =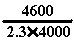 1/2.

Et donc, là aussi on a: 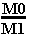= 3.16.

Si M₀ = 200t, alors M₁ = 63.29t ou 63290 kg.

La masse de propergol utilisé est : M₀ - M₁ =136710 kg.

En arrondissant, cela fait environ 15.2 tonnes d'hydrogène, et 121.5 tonnes d'oxygène.

En volume, c'est différent, car l'hydrogène liquide est extrèmement peu dense (70 grammes par litre).

15 tonnes d'hydrogène à 70 gr/l, cela donne : 215000 litres (215 m³).

L'oxygène liquide est très nettement plus dense (1114 grammmes par litre)

121 tonnes d'oxygène à 1114 gr/l, cela donne : 106000 litres (106 m³).

Au total, les propergols stictements destinés à la phase, propulsion par moteur fusée auxilliaire de notre avion, occuperont un volume de : 215+106 = 321 m³, et pèseront 136 tonnes + le poids des réservoirs.

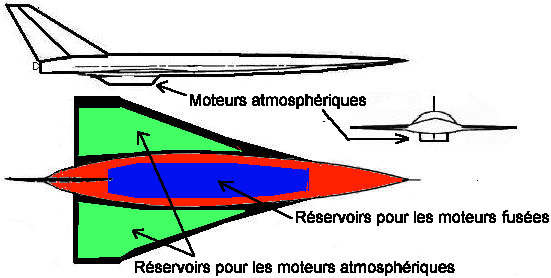
Un avion n'est pas une fusée, et le rapport entre la masse maximum et la masse à vide est bien différente. La faute aux ailes, au système de commandes aérodynamiques, aux moteurs atmosphériques et à leurs réservoirs, au train d'atterrissage etc qui apportent du poids supplémentaire.

Si l'on prend en exemple un avion de la même catégorie de poids (200t) en charge : le B1, sa masse à vide est de près de 80 tonnes.

Pour notre avion spatial, on avait : 200 tonnes moins 136 tonnes de propergols = 64 tonnes pour tout, y compris une éventuelle charge utile et toujours sans compter l'attraction terrestre, ce qui n'arrange pas les choses.

En fait, et compte tenu de tout, on peut au maximum imaginer qu'un engin utilisant, pour sa structure, les matériaux les plus legers et capable de voler, en atmosphère, à plus de mach 10, tout en étant équipé des meilleurs moteurs fusées actuels, pourrait peut-être se satelliser avec pour toute charge utile : le pilote.

Retour à la page: Astronautique 1

Retour à la page: Espace: La propulsion chimique