Rencontre "au sommet" entre un F16 belge et un Mirage 4 français.
Photo: www.mil.be.

LA FORMULE DE PORTANCE

Il est facile de comprendre qu'un air plus dense "portera" mieux qu'un air plus "fin" plus "léger", donc moins dense.

On sait aussi maintenant qu'une aile porte plus ou moins suivant sa cambrure, son angle d'attaque, ou l'utilisation éventuelle de dispositifs hypersustentateurs.

Il est évident que plus une aile est grande, c'est à dire plus sa surface est grande, plus elle "porte".

Enfin, plus l'écoulement est rapide plus la portance est forte tant du point de vue de la formation d'une dépression d'extrados que du point de vue de la déviation d'air vers le bas.

Tout cela pour dire que la portance est un phénomène dépendant de:

  1. La densité de l'air.
  2. Un coefficient dit de portance qui prend en compte le profil de l'aile, son angle d'attaque, et l'utilisation ou non de dispositifs hypersustentateurs.
  3. La surface.
  4. La vitesse.

On obtiendra donc cette formule dépendante de ces variables, (ainsi que celle exprimant la traînée, et qui a la même allure):

Remarque: la surface de référence dépend de ce que l'on calcule.
Par exemple:

PETIT AJOUT FACULTATIF QUE L'ON PEUT DONC IGNORER SI ON N'AIME PAS LES CHIFFRES.

Lorsqu’un avion vole, il «rencontre» l’air, mais cet air n’est pas forcément immobile. Il peut y avoir du vent dans différentes direction.

La vraie vitesse de l’avion par rapport à l’air doit donc tenir compte de ça.

La vitesse ainsi «corrigée», la vitesse dite «air» de l’avion, est la seule qui compte lorsque l’on souhaite calculer la portance par exemple.


Lorsque le flux d’air arrive sur (ou sous) l’aile, sa vitesse change.

Cette vitesse modifiée, on peut la décrire comme étant la vitesse «air» de l’avion multipliée par un coefficient «x» que l’on ne connaît pas.

ce coefficient «x» peut être supérieur à 1 s’il y a accélération (comme sur l’extrados) ou inférieur à 1 s’il y a décélération (intrados).

Pour ne pas mélanger tout, on appellera «x» le coefficient concernant la vitesse sur l’extrados et «y» le coefficient concernant la vitesse sous l’intrados.

On a donc la vitesse sur l’extrados «ve» qui sera égale à la vitesse «air» de l’avion «v» multipliée par x, et la vitesse sous l’intrados «vi» qui sera égale à la vitesse «air» de l’avion «v» multipliée par y. On a donc: ve = v . x et vi = v . y

Selon Bernouilli:

rho g h + 1/2 rho v² = Cte, et rho g h est la pression statique (atmosphérique), mais on sait (voir la page «la portance») que cette pression statique justement est modifiée lorsque la vitesse varie, ce qui est le cas des deux côtés de l’aile.

On a donc des pressions statiques différentes de seulement rho g h sur l’extrados et sous l’intrados.

Si l’on veut exprimer les pressions statiques à ces endroits, on ne peut plus utiliser simplement rho g h, mais un terme plus général comme Pstat e (pression statique extrados) et Pstat i (pression statique intrados).

L’équation

rho g h + 1/2 rho v² = Cte

devient, pour l’extrados:

Pstat e + 1/2 rho ve² = Cte

Et pour l’intrados:

Pstat i+ 1/2 rho vi² = Cte


Bernouilli nous dit que la pression totale est constante, donc:

Pstat e + 1/2 rho ve² = Pstat i+ 1/2 rho vi²



La pression statique résultante sur l’aile est la différence de pression entre l’intrados et l’extrados, et celle de l’intrados étant supérieure à l’autre, on calculera la différence comme ceci:

Pstat i - Pstat e = 1/2 rho vi² - 1/2 rho ve²


Mais puisque ve = v . x et vi = v . y

On a:

Pstat i - Pstat e = 1/2 rho v²y² - 1/2 rho v²x²

Qui donne:

Pstat i - Pstat e = 1/2 rho (v²y² - v²x²)

Et même:

Pstat i - Pstat e = 1/2 rho v² (y² - x²)

La pression globale résultante (Pg) sur les ailes est donc

Pg = 1/2 rho v² (y² - x²)

Une pression, c’est une force sur une surface, et donc une force, c’est une pression fois une surface.

La force de portance vaut donc le produit de la pression par la surface (des ailes).

On a alors:

F = Pg . S = 1/2 rho v² S (y² - x²)

Ce y² – x² représente en fait la capacité de l’aile à créer une différence de vitesse, entre l’extrados et l’intrados, et cette capacité dépend du profile de l’aile, en y incluant aussi bien l’incidence* que les dispositifs hypersustentateurs*.

(*) Plus l’incidence augmente, plus l’air passant sur l’extrados est accéléré par la dépression qui augmente (revoir «la portance» page 2), et parallèlement l’air passant sous l’intrados ralenti aussi.

Les dispositifs hypersustentateurs ont une action pcomparable à la prise d’incidence (en particulier les volets) et eux aussi modifient la vitesse d’écoulement.

Cette capacité de l’aile à créer une différence de vitesse, entre l’extrados et l’intrados, ou cette capacité de l’aile à créer plus ou moins fortement de la portance, c’est le coefficient de portance, et on le représente souvent par Cl (coefficient of lift) ou Cz (parce que l’axe vertical est traditionnellement l’axe Z.

La formule ci dessus devient donc: F = 1/2 rho v² S Cl ou F = 1/2 rho Cl S v²


FIN DU PETIT AJOUT FACULTATIF



On représente l'évolution de la portance suivant l'angle d'attaque comme ceci:

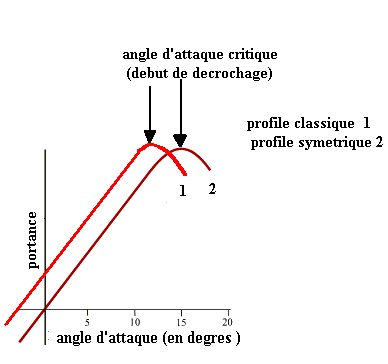
Remarquez l'aile à profil symétrique qui pour un angle nul a une portance nulle alors que le profil classique offre déjà une portance à 0° d'angle d'attaque.

La portance, la traînée, la traction et le poids peuvent être représentés comme ceci pour bien visualiser le problème:

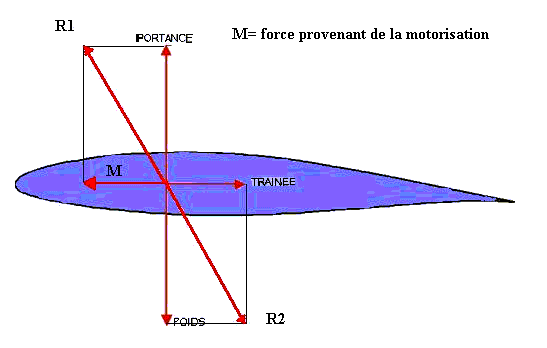
Il suffit alors que la "bonne" résultante (R1) l'emporte sur la "mauvaise" (R2) pour gagner.

Remarque: pendant une phase de vol strictement horizontale à vitesse strictement constante, il suffit que la portance soit exactement égale au poids, et que la force motrice soit exactement égale à la traînée, ce qui donne alors R1 = R2.

Sur ce dessin, la potance et le poids sont sur la même ligne pour simplifier le calcul; ce qui n'est pas le cas dans la réalité comme nous le verrons au chapitre dédié à l'équilibre des avions.