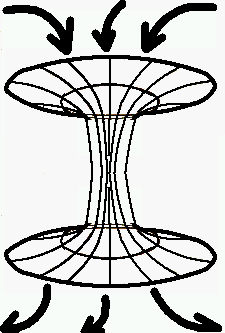
On a dit qu'il était impossible de voyager à une vitesse égale et à fortiori supérieure à la vitesse de la lumière (C). Oui, mais... dans l'espace temps!

Prenons un exemple:
À une époque où le bateau était le seul moyen de franchir les mers, il était déraisonnable de penser que l'on pourrait, un jour, traverser l'atlantique en quelques heures.
Aucun navire ne pourrait réaliser une telle prouesse parce que la résistance de l'eau entraînerait sur la coque du bateau des contraintes mécaniques insupportables, et, en plus, il faudrait des moteurs d'une puissance insensée toujours à cause de la résistance de l'eau.

L'histoire nous montre que le problème fût "contourné par le haut", grâce à l'aviation.

Image: Arpingstone.

La question est: peut-on contourner l'espace-temps, ou tout au moins, voyager autrement que dans l'espace-temps?

Le Warp Drive.

C'est une solution proposée par Miguel Alcubiere.
On commence par créer une "bulle", ou une "vague" d'espace-temps autour du vaisseau, cette "bulle" ayant pour objectif de l'isoler, de le placer dans une sorte de microespace-temps séparé du nôtre, et dans lequel le vaisseau ne bouge pas, donc ne dépasse certainement pas la vitesse de la lumière!

Ensuite, on "comprime" l'espace-temps devant cette "bulle" en générant un champs gravitationnel gigantesquissime, une sorte de gouffre gravitationnel, en amont.

Enfin, on "dilate" l'espace-temps derrière la "bulle" en générant, cette fois, un puissant champs de "gravitation négative", ou répulsive, un "pic" gravitationnel en quelque sorte, en aval.

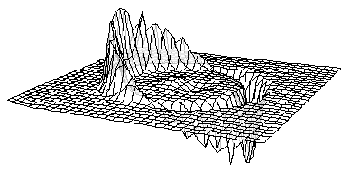
Image: NASA.

Une autre vue, avec le vaisseau.

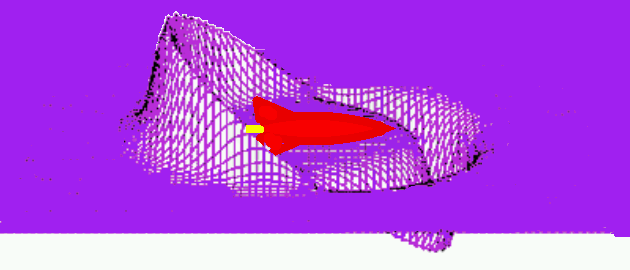
À partir de la bulle, ou de la vague d'espace-temps dans, ou sur laquelle le vaisseau est immobile, on déforme donc notre espace temps (on le plie devant, pour l'étendre derrière) de manière à le traverser sans que cela soit vraiment assimilable à un déplacement dans notre espace-temps.

Résultat?
Pour certains: la porte ouverte aux voyages intergalactiques à l'équivalent de milliers de fois la vitesse de la lumière, lorsqu'on maîtrisera la technique, et ce n'est de toute façon pas pour demain, pour d'autres: trop de problèmes subsitent pour pouvoir trancher.

Lesquels?

Si l'on retire ceux qui pensent que cette théorie ne repose sur rien de concret, et ceux qui pensent que ce n'est pas impossible en théorie, mais que ça réclamerait une quantité d'énergie (*) proprement astronomique (voir même, peut-être plus que l'univers visible n'en contient), il en reste très, très peu pour parier dessus.

(*)Il s'agit de l'énergie qui doit servir à déformer l'espace-temps pour former la "bulle", et celle qui doit servir à générer le champs gravitationnel et son contraire.

On le sait maintenant, l'espace-temps est déformable.

La relativité générale décrit d'ailleurs la gravitation comme une déformation de l'espace-temps induite par la présence d'une masse.

Pour représenter un champs gravitationnel en temps que déformation de l'espace-temps, on a souvent recours à des dessins de ce genre:

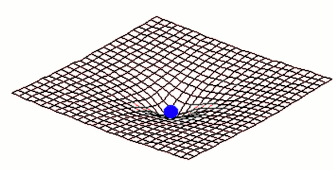
Une masse déforme l'espace-temps, dans les quatre dimensions, comme cette boule bleue déforme ce tissus en deux dimensions seulement.

Attention à ne pas se tromper, ce dessin 2D est censé faire comprendre le concept de déformation pas de représenter une quelconque réalité dans la forme ou l'aspect concret de l'espace-temps à proximité d'une masse.

Sur une surface comme celle-ci, tout objet passant à proximité voit sa trajectoire modifiée par la déformation.

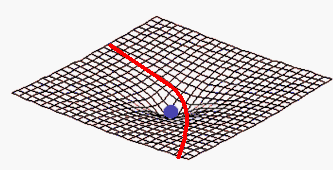
Autour d'une masse, l'espace-temps est déformé, oui mais il ne s'agit pas d'un "creux" comme sur le dessin ci dessus, mais d'une déformation qui se fait tout autour de la masse, en trois dimensions (et même en quatre parce que le temps lui-même est influencé par la gravitation).

De cette façon, la déviation de la trajectoire des objets passant à proximité donne quelque chose comme ça:

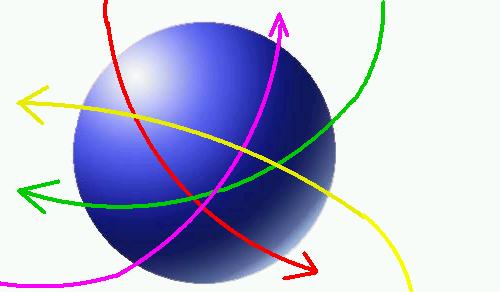
Les objets suivent en fait une ligne droite, mais c'est l'espace-temps lui-même qui est courbé.

Puisque c'est l'espace-temps qui est courbé, alors la gravitation ne concerne pas seulement les objets possédant une masse, mais elle concerne aussi la lumière!

En passant à côté d'un astre, la lumière est donc déviée.

Cette conséquence de la relativité générale fût confirmée à l'occasion d'une éclipse.
Une fois le disque solaire masqué de manière à ce que les astronomes ne soient plus gênés par sa luminosité extrême, une étoile devant se trouver derrière le soleil (étoile connue dont la position précise était connue), et donc être invisible est apparue visible à côté du disque solaire.

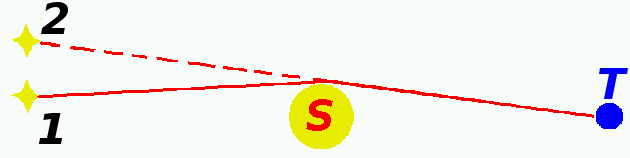
La "vraie" position de l'étoile est en 1, et la courbure des rayons lumineux fait que, de la Terre, en suivant une ligne de visée droite, elle semble être en position 2.

Plus une masse est importante, plus elle courbe l'espace-temps.

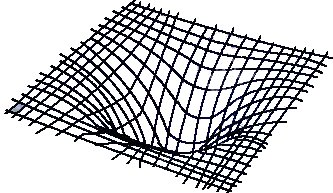
En deux dimensions, on représentera la chose par un "creux" plus prononcé.

En regardant cela sous un autre angle, ça donne ça:

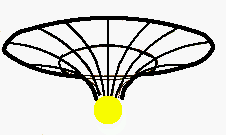
Pour une masse donnée, la courbure maximale de l'espace temps est atteinte à proximité immédiate, au "contact" de l'objet massique (et pas à l'intérieur).

De plus, on sait depuis Newton que la force de gravitation varie comme le carré de la distance par rapport au centre de gravité.
La variation est du genre: F=G*M1*M2/d².
Avec:
G= constante gravitationnelle=6,6742*1011.
M1et M2= les deux masses en interaction gravitationnelle.
d= la distance entre les centres de gravité des deux masses M1 et M2.


On obtiendra donc une déformation de l'espace-temps plus importante avec un objet plus compacte, plus dense, parce qu'à masse égale, on peut s'approcher d'avantage de son centre de gravité sans pénétrer à l'intérieur (rayon plus petit, donc d possible plus petit).

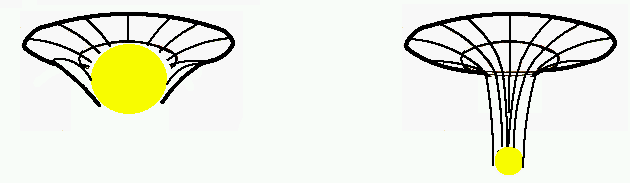
Sur cette image sont représentées deux masses de même valeur mais de rayon différents; la plus compacte des deux, celle dont le rayon est le plus petit (à droite), déforme d'avantage l'espace à son voisinage immédiat (le dessin représente un "trou" plus profond aux paroi plus "pentues").

Et je répète donc que ces dessins 2D sont censés faire comprendre le concept de déformation pas de représenter une quelconque réalité dans la forme ou l'aspect concret de l'espace-temps à proximité d'une masse.

Quelques précisions de plus ici.

Vitesse de libération.

Si l'on tire une balle de fusil verticalement vers le ciel, elle va s'élever en perdant de la vitesse, et, à force de perdre de la vitesse, finira par s'arrêter et retomber.

Plus la vitesse de la balle est élevée, plus l'altitude atteinte avant de retomber est élevée.

Il éxiste une vitesse à partir de laquelle la gravitation (qui diminue comme le carré de la distance) ne pourra jamais complètement arrêter la balle, et celle-ci échappera donc définitivement à la Terre.

Cette vitesse, c'est la vitesse de libération, pour la Terre, elle est d'environ 11,2 Km/sec, soit un peu moins de 40.000 Km/h.

Cette vitesse est, sur la Terre, unique et valable pour tous les corps, cela signifie que n'importe quel objet, et quelque soit sa masse, qui quitte la Terre à 11,2 Km/s ne retombera pas, et s'éloignera à tout jamais.

La vitesse de libération dépend de la masse et de la densité de la planète, elle varie donc d'un astre à l'autre.
Exemple:
Pour la Lune, la vitesse de libération est de: 2,4 Km/s. Pour Vénus: 10,4 Km/s. Pour Mars: 5 Km/s.





Pourrait-il éxister un objet si massif et si compacte qu'il serait capable de déformer l'espace-temps proche si fortement qu'aucun objet ne pourrait échapper à sa gravitation (vitesse de libération supérieure ou égale à la vitesse de la lumière), et que la trajectoire d'un rayon lumineux passant à proximité ne serait pas simplement déviée, mais complètement recourbée au point de "tomber", si l'on peut dire, sur cet objet?

Ce type d'objet existe, et on appelle ça un trou noir.

Côté illustration, on le représenterait comme ça:

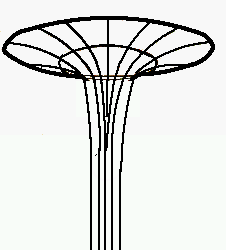
Les parois de "l'entonnoir" sont verticale, et aucun astre n'y est représenté, écrasé sous sa propre gravité, il est théoriquement réduit à un point.

Comme il est très difficile d'expliquer comment la masse de parfois plusieurs milliers (voir millions) d'étoiles peut être concentrée en un point de taille nulle, on dit plutôt une singularité.

Seulement, voilà, il pourrait exister une autre possibilité, c'est qu'à la place d'une sorte de cul-de-sac sans autre issue que l'écrasement total, on ait un passage vers un autre endroit de l'espace-temps.