On voit régulièrement des gens qui croient qu'il est possible de propulser un engin sans rien éjecter du tout, simplement en accélérant, par exemple le long d'un rail, une masse située à l'intérieur de l'engin, l'arrêter, la ramener tout doucement au point de départ, et ainsi "réarmer" le système pour pouvoir recommencer. À chaque fois que la masse est très fortement accélérée dans un sens, le "vaisseau" est accéléré dans l'autre sens (action>>>réaction), mais que se passe-t-il ensuite, lorsque la masse est freinée et arrêtée, ainsi que lorsqu'elle est ramenée (même tout doucement) au point de départ?
Y-a-t-il un mouvement qui l'emporte sur les autres? en ralentissant la masse en douceur, et en la ramenant avec précaution, peut-on éviter que ces mouvements n'annulent l'effet du premier? En d'autres termes: peut-on se propulser ainsi?

Voici un exemple type de ce genre de système, qui pour clarifier l'explication, sera chiffré.

La masse (m) de 10 tonnes (par exemple en acier) se déplace, dans un premier temps, sur une distance (x) de 20 mètres en étant soumise à une force (F) de 100.000N (venant, par exemple, d'un très puissant aimant), avant d'être ralentie et arrêtée sur une distance de cinquante mètres (c'est à dire plus doucement).

Cette force lui communique donc une accélération de: a = F/m = 100.000/10.000 = 10m/s².

On peut trouver le temps que dure ce déplacement de 20 mètres en utilisant l'équation: x = 1/2*a*t², on a:
20 = 1/2*a*t² = 1/2*10*t², donc t² = (20/10)*2 = 4, et t = 2 secondes.

En réaction, le "vaisseau" reçoit donc lui aussi une force de 100.000N pendant un temps de 2 secondes.

La masse du "vaisseau" étant de 100 tonnes, la force de réaction de 100.000N lui communiquera une accélération de: a = F/m = 100.000/100.000 = 1 m/s².

La distance (x1) que le vaisseau va parcourir pendant que cette force de 100.000N agit, c'est à dire pendant un temps de 2 s (donc t² = 4) peut être calculée par l'équation:

x1 = 1/2*a*t², avec a = 1m/s, et t² = 4, on a donc:
x1 = 1/2*1*4 = 2m.

Le "vaisseau" se déplace donc de 2 mètres pendant que la force agit.

La vitesse maximale atteinte par le vaisseau en fin d'accélération est de: V = à*t = 1*2 = 2 m/s.

La vitesse maximale atteinte par la masse en fin d'accélération est calculable grâce à l'équation: V = a*t, ce qui donne, dans ce cas ci: V = 10*2 = 20 m/s.

Ensuite, la masse est ralentie et arrêtée moins brutalement qu'elle n'a été accélérée, c'est à dire sur une distance de 50 mètres.
La masse décélère donc depuis une vitesse de 20 m/s jusqu'à une vitesse de 0 m/s (l'arrêt) sur une distance de 50 mètres.
La décélération étant constante, la vitesse moyenne de la masse pendant son freinage vaut 20 : 2 = 10 m/s.

Le temps que met la masse à parcourir les 50 mètres de distance de décélération est donc de: 50 : 10 = 5 s.

On peut donc maintenant calculer la décélération (accélération négative) qu'il faut imprimer à la masse pour l'arrêter en 5 secondes alors que sa vitesse est de 20 m/s, pour cela, on utilise l'équation: V(final) = V(initial) - a*t.
V(final) = 0 (arrêt), V(initial) = 20 m/s, et t = 5 s.
On a donc: 0 = 20 - a*5, donc -20 = -5*a, donc 5a = 20, donc a = 4 m/s².

La force nécessaire à ce ralentissement est donc de: F = m*a = 10.000*4 = 40.000N.

En réaction le vaisseau reçoit donc lui aussi une poussée, orientée vers l'arrière et donc "freinante" de 40.000N pendant 5 secondes.
Décélération communiquée au vaisseau par 40.000N pendant 5 secondes: a = F/m = 40.000/100.000 = 0,4 m/s².
Vitesse atteinte par le vaisseau (qui souvenez-vous, avait atteint la vitesse de 2 m/s) après la phase de décélération à 0,4 m/s² pendant 5 secondes: V(final) = V(initial) - 0,4*5 = 2 - 2 = 0.

On constate donc que même en ralentissant la masse assez doucement jusqu'à l'arrêt, on a communiqué au vaisseau une décélération telle pendant un temps tel que cela a provoqué aussi l'arrêt du vaisseau.

Notre vaisseau est donc à l'arrêt, en ralentissant la masse moins violemment qu'on ne l'avait accélérée, on a produit une force de ralentissement sur le vaisseau qui était certes moins forte que lors de l'accélération, mais qui, par contre, a duré plus longtemps. Au total, il y avait équivalence, et tout naturellement, toute la vitesse obtenue a été perdue.

pendant la période de freinage, le vaisseau a parcouru une certaine distance, cette distance (x2) est de:
x2 = 1/2*a*t² = 1/2*0,4*5² = 1/2*0,4*25 = 0,2*25 = 5 mètres.

Au total, le vaisseau s'est déplacé de 2 mètres pendant sa phase d'accélération, et de 5 mètres pendant sa phase de freinage, donc de 7 mètres en tout avant de....... s'arrêter!

Première constatation: on ne peut pas vraiment se propulser ainsi puisque le vaisseau est de nouveau à l'arrêt, mais maintenant, il faut se poser la question de savoir s'il ne serait pas au moins possible de progresser par bond. Pour cela il faut "réarmer" le système en ramenant la masse, au point de départ.

Lors du "réarmement", la masse de 10 tonnes est tout doucement ramenée au point de départ, si doucement que l'on met environ 37,5 secondes, à lui faire parcourir les 70 mètres qui la sépare du point de départ.
Puisque t vaut un peu moins de 37,5 s, alors t² = 1400

De l'équation: x = 1/2*a*t², on peut trouver l'accélération qui vaut: a = (x*2)/t²
On sait que x vaut 70 mètres, et t² vaut 1400.
Donc a = (70*2)/1400 = 140/1400 = 0,1 m/s².

La force nécessaire à faire ce travail sera de F = m*a = 10.000*0,1=1000N.

En réaction le vaisseau recevra donc lui aussi une force de 1000N mais en sens inverse cette fois, ce qui lui communiquera une accélération (vers l'arrière) de :
a = F/m = 1000/100.000 = 0,01 m/s².
Cette faible accélération lui sera appliquée aussi longtemps que durera le "réarmement",

Pour calculer la distance de recul, on utilise l'équation:
x = 1/2*a*t², avec a = 0,01 m/s², et t² = 1400.
Donc cette distance de recul est de x = 1/2*0,01*1400 = 7 mètres!!!!! (la même distance que celle parcourue en avançant!!)

La vitesse atteinte par la masse en revenant à son point de départ et après une accélération de 0,1m/s² sur 70 mètres est de: V = a*t = 0,1*37,5 = 3,75 m/s
La vitesse de recul atteinte par le vaisseau lorsque la masse est revenue à son point de départ est de V = a*t = 0,01*37,5 = 0,375 m/s
À ce moment la masse est revenue à son point de départ, et comme je n'ai rien prévu pour la freiner, elle vient percuter violemment une butée.

Cette fois on est dans le cas d'une décélération très très forte, une véritable collision, la masse passe d'une vitesse de 3,75 m/s à 0 m/s en, disons, 2 centièmes de seconde, ce qui représente une décélération de: différence de vitesse (3,75) divisé par différence de temps (0,02) = 3,75/0,02 = 375/2 = 187,5 m/s².

La force exercée par cette brutale décélération est de F = m*a = 10.000*187,5 = 1875000N
Par réaction le "vaisseau" reçoit lui aussi une force de 1875000N pendant 0,02 secondes.
La masse du "vaisseau" étant de 100 tonnes, il reçoit une accélération (vers l'avant cette fois) de a = F/m = 1875000/100.000 = 18,75 m/s² pendant 0,02 secondes.
Avant l'impact de la masse sur sa butée, le "vaisseau" était en train de reculer à la vitesse de 0,375 m/s, l'impact lui donne une accélération vers l'avant, donc en sens inverse de son mouvement actuel en conséquence de quoi le calcule de la vitesse après impact devra se faire en considérant l'accélération produite par l'impact comme négative (puisque de sens contraire au mouvement).
Sa vitesse après impact est donc de: V(final) = V(initial) - a*t = 0,375 - 18,75*0,02 = 0,375 - 0,375 = 0!!!
L'impact a donc provoqué l'arrêt total.

En résumé, et jusqu'à présent, le "vaisseau" a avancé de 7 mètres, s'est arrêté puis reculé de...7 mètres et s'est arrêté de nouveau!

L'aller-retour de la masse s'est fait en 4 étapes:

1. accélération forte (sur les 20 premiers mètres)
2. décélération faible (sur les 50 derniers mètres)
3. accélération très faible (réarmement)
4. décélération très très très forte (impact final)

Une décélération n'étant rien d'autre qu'une accélération négative, on peut chaque fois remplacer le terme "décélération" par "accélération" (négative bien sûr).
On a donc 4 accélérations différentes de très faible à très très très forte, mais avec à chaque fois le même résultat: chaque étape, quelque soit l'accélération choisie, annule l'effet de la précédente!

Mais il y a mieux encore, la masse mobile à l'intérieur de la fusée fait un dixième du poids total de la fusée (10t/100t), et lorsqu'elle se déplace dans un sens, sur une certaine distance, la fusée, dix fois plus massive, se déplace dans l'autre sens mais sur une distance 10 fois plus faible (70m/7m), la conséquence de cela, c'est que si l'on place à l'extérieur de la fusée un point de repère en face du centre de gravité de la fusée, on s'aperçoit que, malgré les apparents déplacement de la fusée, son centre de gravité reste constamment en face du même point de repère.
Le centre de gravité n'ayant pas bougé d'un poil, on peut en déduire que la fusée elle même n'a de fait, pas bougé d'un poil, sa "carcasse" a simplement oscillé autour de son centre de gravité resté fixe.

On ne peut décidément rien contre la conservation de la quantité de mouvement.

Voici maintenant une variante qui m'avait été proposée comme devant théoriquement supprimer le risque de recul lors du réarmement (Il y en aura toujours pour croire que l'on peut contourner le principe de conservation de la quantité de mouvement en complexifiant le système).

Il y a cette fois deux masses d'aciers, sur deux rails; elles sont tous les deux attirées par un très puissant électro-aimant, et coulissent le long de leur rail respectif.
La différence avec le précédent système c'est que cette fois elles seront ramenées vers l'avant par un mouvement de "pivotement" du rail, l'auteur du système étant persuadé qu'en faisant tourner les deux rails dans des sens différents, il évite ainsi l'effet de recul.
Mais voyons cela de plus près.

Dans un premier temps, l'électro-aimant est allumé, attirant puissamment les deux masses d'acier à lui.

Dans un deuxième temps, les deux masses sont ramenées vers l'avant comme représenté sur le dessin ci dessous.

C'est ce mouvement de rotation qui était présenté comme capable d'éviter le recul de la fusée, sous prétexte que les deux masses tournent en sens contraire.

L'ennui, c'est que les deux masses ont beau tourner dans deux sens différents, il n'en reste pas moins qu'elles partent toujours de l'arrière pour aller vers l'avant, et qu'il y a donc une composante de leur mouvement qui, pour toutes les deux, est strictement d'avant en arrière.

Pour mieux comprendre, faisons une comparaison avec une situation qui nous est plus familière.
Remplaçons les deux masses par deux haltères, et les deux rails pivotants par les bras d'un athlète.

Au départ, les deux masses sont côte à côte à l'extrémité de leur rails respectif.
Ce qui se traduit par: l'athlète tient les deux haltères aux bout de ses bras tendus devant lui.
Comme sur ce dessin:

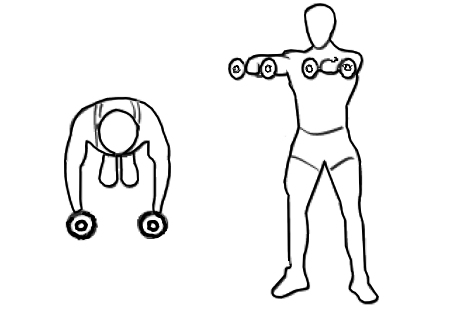
Ensuite les deux rails pivotent de manière à amener les deux masses vers l'avant.
Pour un athlète normal, sans une souplesse extraordinaire, il est difficile d'imaginer qu'il puisse amener ses deux bras depuis la position "tendus devant lui" jusqu'à la position "tendus derrière son dos", alors nous nous contenterons de lui demander d'amener ses bras jusqu'à la position: "tendus écartés de chaque côté"
Comme sur ce dessin:

Il suffit d'essayer pour se ressentir immédiatement une force vers l'avant lors du mouvement des bras de l'avant vers l'arrière, et cela, bien que les bras décrivent des arcs de cercle avec un sens de rotation différents l'un de l'autre.

Il n'y a donc aucune compensation, et cette approche (mouvements circulaires) n'apporte rien de plus que la première (trajectoire rectiligne sur un rail).

On ne peut obtenir aucune propulsion avec un système ne respectant pas le principe de conservation de la quantité de mouvement. Il faut donc TOUJOURS soit éjecter quelque chose (propulsion par réaction) soit recevoir de l'extérieur une quantité de mouvement supplémentaire (propulsion par voile).

Page précédente