Le rayonnement de fond cosmologique, ou fond diffus cosmologique.

Dans les premiers temps du Big Bang, l'univers était rempli de rayonnements, et de particules diverses formant un plasma. Ces rayonnements étaient "piégés" par le plasma avec lequels ils interagissaient sans cesse.
Lorsque la température de l'univers est devenue suffisamment basse les électrons de se sont liés aux noyaux d'atomes déjà formés (essentiellement de l'hydrogène).
Le plasma qui piégeait la lumière laissa alors sa place à un gaz neutre et transparent, et la lumière fut "libérée", c'était environ 300.000 ans après le début du Big Bang.
Ces rayonnements remplissant tout l'univers continuent encore a nous parvenir avec une longueur d'onde fortement allongée par l'expansion de l'univers, c'est le fond diffus cosmologique ou CMB (Cosmic Microwave Background). La longueur d'onde actuelle du CMB se situe dans la gamme des micro-ondes.
La découverte de ce rayonnement fut une preuve de plus de la validité du Big Bang.

La théorie du Big Bang s'accomode tout aussi bien d'un univers infini ou fini, étonnant? Non, non.

Première possibilité: il est infini, et l'a.......toujours été!
Dans ce cas, aux premiers instants du Big Bang, l'univers était extrêmement dense, extrêmement chaud, et..... infini!
Alors me direz-vous comment peut-il subir une expansion, accompagnée d'une baisse de la densité, en d'autre terme où trouve-t'il la place pour "faire du vide"?

On peut voir l'expansion d'un univers infini comme un zoom sur un essaim d'abeilles; avant, l'essaim semble presque compacte, mais pendant que l'on fait le zoom, les abeilles semblent s'écarter les unes des autres. Bien sûr ce n'est qu'une image, et le problème de la place libre dans un univers infini et dense demeure, alors voilà une autre comparaison amusante pour montrer qu'on trouve toujours assez de place dans un espace infini même s'il est déjà plein.

Imaginez un hotel contenant un nombre infini de chambres toutes occupées. Brusquement, tous les clients de l'hotel reçoivent l'ordre de quitter leur chambre pour rejoindre la chambre dont le numéro est le double de leur chambre "d'origine".

Tous les nombres peuvent être multipliés par deux, donc tout le monde trouvera une nouvelle chambre avec un numéro de chambre double de l'ancien.
Tout client arrivant dans une nouvelle chambre la trouvera libre puisque son ancien locataire sera parti pour la chambre dont le numero est double de celle-ci, il n'y aura donc aucun client sans chambre.

MAIS, les nouvelles chambres occupées portent TOUTES un numéro valant deux fois quelque chose, donc TOUTES les chambres nouvellement occupées portent un numéro PAIR. Nous avons donc "libéré" tous les numéro impairs, et donc nous avons fait de la place. On pourrait remplir toutes ces chambres impaires désormais libres et.... les libérer à nouveau en recommençant le même manège.
Voilà comment on fait de la place dans un espace infini déjà plein.

Imaginons maintenant que toutes les galaxies de cet univers s'éloignent les unes des autres à une vitesse à peu près constante (appelons la V), que verrions nous?

Nous verrions une galaxie proche (appelons la G1) s'éloigner de nous à cette vitesse V, mais comme la galaxie suivante (appelons la G2) s'éloigne de G1 à cette même vitesse V, alors G2 s'éloigne de nous à la vitesse V+V= 2V. Nous verrions donc les galaxies s'éloigner de nous à une vitesse d'autant plus grande qu'elles sont déjà éloignées, ce qui est conforme aux observations.

Deuxième possibilité: l'univers est fini.
Dans ce cas, aux premiers instants du Big Bang, l'univers était extrêmement dense, extrêmement chaud et.....extrêmement petit! Tellement petit que l'ensemble de l'univers pouvait être comprimé dans une petite sphère de.....10^-33cm, un millionnième de milliardième de milliardième de milliardième de cm, ou: 0,000000000000000000000000000000001cm! fameuse densité n'est-ce pas!
En desssous de cette taille, aucune théorie valide n'éxiste, et on ne sais même pas si cela aurait un sens ni même si l'univers a réellement connu une dimension plus petite que celle là.

Un univers fini serait donc parti de.... "trois fois rien sous forme d'une petite boule", pour arriver à ce que nous connaissons aujourd'hui.
Un univers fini doit aussi être conforme aux observations, en particulier au fait que les galaxies doivent s'éloigner de nous d'autant plus vite qu'elles sont loins.

Pour faire comprendre facilement comment il est possible d'obtenir une augmentation de la vitesse de récession des galaxies avec l'éloignement, tout en décrivant un univers fini, mais sans limites, c'est à dire sans qu'il soit possible d'arriver à un bord ou une fin, certains ont choisi l'analogie avec le ballon que l'on gonfle.

Si l'on dessine des galaxies sur un ballon et qu'on le gonfle, on les voit s'éloigner les unes des autres, et de plus, les galaxies "voisines" sur le ballon s'écartent moins vite que celles qui ne sont pas du même côté, donc: plus elles sont loin plus elles s'éloignent vite (ce qui est conforme aux observations). Et enfin, la surface d'un ballon est finie mais elle n'a pas de limite, de frontière, de bord.
Pas de bord, d'accord, mais seulement si l'on fait l'effort de s'imaginer réellement en deux dimensions, et ce n'est pas évident.
Le modèle ballon n'est qu'une image, au même titre que l'hotel au nombre infini de chambre, il ne doit surtout pas nous faire imaginer que l'univers en expansion ressemblerait à ça:

C'est à dire un univers dans lequel les galaxies (en jaune) se répartiraient réellement à la périphérie d'une sphère qui se dilate. L'univers ne ressemble pas à cela.

Dans ce genre de représentation de l'univers il y a des bords, des frontières ,des limites (choisissez le terme que vous préférez): la surface extérieure de la sphère, et la surface de la sphère intérieure. Ce qui amène certains à se demander ce qu'il y a, vers l'extérieur, après le "front" d'expansion des galaxies, et ce qu'il y a, en direction du centre, avant le "front" de galaxie. Comme le modèle est absolument faux, aucune réponse n'a de sens.
Si l'univers est fini, alors il n'a aucun bord, voyons comment un univers fini peut-être sans bords.
Commençons d'abord par imaginer la chose dans un espace à deux dimensions.
L'espace à deux dimensions "type", c'est le plan, un espace à deux dimension "type" fini, c'est plutôt un grand carré.
Attention! Pour pouvoir se représenter un espace à deux dimensions, il ne suffit de s'imaginer sur une surface plane; il faut, en plus:

1. Etre sois même en deux dimensions, c'est à dire à l'état d'image, de dessin.
2. Ne recevoir aucune informations de la troisième dimension, comme si la seule "lumière" que vos "yeux" puisse recevoir, circulait exclusivement sur le plan.

Dans ces conditions, si le "carré" qui représente votre espace fini est replié et déformé pour former une sphère, vous aurez l'impression de vivre dans un univers assez curieux. Il n'y aurait aucun bord, aucune limites, mais en se déplaçant continuellement dans la même direction, vous reviendriez systématiquement au point de départ.

C'est un peu ce qui se passe lorsque l'on se déplace sur la Terre, à ceci près que le fait que nous soyons nous même en trois dimensions nous a permis de bien comprendre le pourquoi et le comment, en regardant une simple boule.
Mais des êtres réellement en deux dimensions vivant à la surface d'une sphère ne pourraient se représenter cette forme faisant appel à un nombre de dimension supérieur à leur univers habituel.
C'est ce qui nous arrive à nous aussi lorsque nous essayons d'imaginer un univers à trois dimensions fini mais sans limite.
Essayons:
Prenons un espace fini à trois dimensions tout simple: un cube.

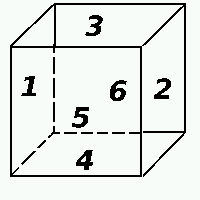
Repérons les faces: gauche (1), droite (2), dessus (3), dessous (4), avant (5), et arrière (6).
Si je décide d'étirer et de replier mon cube de manière à faire coïncider les faces 1 et 2, je supprime ainsi deux limites, car si l'on veut sortir par la face 1, on rentre en fait par la face 2. La nouvelle forme ainsi obtenue est un anneau de section carrée.

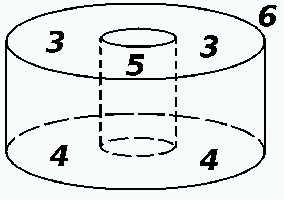
Les faces 3 et 4 sont devenues des disques évidés au centre, les faces 5 et 6 sont respectivement l'intérieur et l'extérieur de l'anneau.
En étirant et en repliant mon anneau, je peux faire coïncider les faces 3 et 4, supprimant encore deux autres "frontières".

Une fois les faces 3 et 4 jointes, j'obtient ce que l'on appel un tore, et il ne me reste plus que les "faces" (si l'on peut encore les appeler ainsi) 5 et 6.

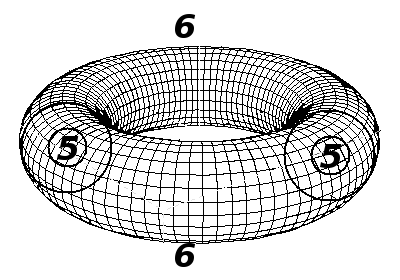
La "face" 5 constitue l'intérieur du tore, et la face 6 l'extérieur. Maitenant, pour réaliser un espace à trois dimensions fini sans limites, il ne me reste plus qu'à...... hum.... faire coïncider les faces 5 et 6!?!???????...Pas facile, mais pas impossible...... mathématiquement bien sûr!

Je vais essayer par une autre voie: j'étire et je déforme mon cube de base pour obtenir un disque épais où les faces 1, 2, 3, et 4 son confondues dans la circonférence du disque. Les deux faces du disques correspondent alors aux faces 5 et 6 du cube.

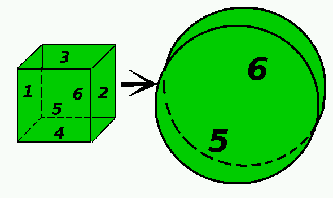
Je déforme ("j'incurve") ensuite ce disque, la circonférence se "refermant" sur elle-même, pour obtenir une sphère creuse comme ceci:

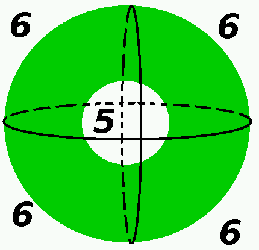
La face 5 correspond maintenant à l'intérieur de la sphère, et la face 6 à l'extérieur.

Pour obtenir un univers fini sans limite, je dois encore faire correspondre les faces 5 et 6..... et....c'est pas plus facile que dans le cas du tore!!! Et pourtant notre univers, s'il est fini, est bien sans bord.

C'est donc possible, mais nous ne sommes pas capable de nous représenter intellectuellement ce que cela donne.
Les êtres en deux dimensions dont nous parlions plus haut ne pouvaient s'imaginer ce qu'est une sphère parce qu'elle se "courbe" dans une dimension qu'il leur est étrangère et inaccessible..
De même, notre univers à trois dimensions spatiales (plus une de temps) peut être courbé de manière à ce que toute limite disparaisse sans que nous soyons capable de nous en faire une image.
Plus surprenant encore, il n'est mathématiquement pas nécessaire qu'il éxiste une dimension supplémentaire pour y effectuer la contorsion, étonnant non?

Tout cela n'avait donc d'autre but que de faire oublier notre conception ancienne, intuitive, et....... fausse de notre univers.
Partant de là, il est plus facile d'accepter l'idée de voyager en "manipulant" l'univers, enfin si toutefois il n'est pas insensé d'imaginer que ce genre de chose puisse être un jour à notre portée!