AccueilGallerieDefence daysLiens

Pour pouvoir aller plus loin dans des délais raisonnables il faudrait pouvoir y aller très, très, très vite, ce qui n'est déjà pas facile, même pour des vitesses inférieures à celle de la lumière (représentée par la lettre "C"), mais est TOTALEMENT EXCLU pour des vitesses supérieures à C (car de telles vitesses sont totalement impossibles).

Tout le monde, ou presque, a déjà entendu dire que la vitesse de la lumière est une limite infranchissable. Il y en a déjà moins qui savent vraiment pourquoi, il y en a même qui donnent, sur ce sujet, des explications totalement erronées issues de livres (voir de BD) de science-fiction.

Exemple d'explication "science-fictionnesque": lorsqu'un vaisseau atteint la vitesse de la lumière, il perd son énergie!!!
Une variante existe disant qu'il se transforme en énergie!!!!
Tout cela n'est que pure invention.

Cette limitation de vitesse tire son origine de la théorie de la relativité.

Deux exemples pour bien cerner le problème:

1) La quantité de mouvement.

On exprime souvent la quantité de mouvement d'un objet par la formule: P=mv, ou plus exactement, et parcequ'il s'agit d'une grandeur vectorielle: .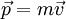

Si cette expression est valable dans les conditions de la vie de tous les jours, elle ne l'est plus lorsque les effets relativistes commencent à se faire sentir, en d'autre terme aux très hautes vitesses.
Dans ces conditions, l'expression de la quantité de mouvement devient: 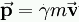(lire: P égal gamma m v).

Avec: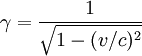

Avec v=vitesse de l'objet, et c=vitesse de la lumière.

Vous remarquerez tout de suite que lorsque la vitesse de l'objet devient égale à celle de la lumière, on a : v=c, donc le rapport v/c=1, donc (v/c)²=1, donc 1- (v/c)²=0, donc racine carrée de (1-(v/c)²)=0, donc gamma devient égal à 1/0 ce qui équivaut à..... l'infini!!

La quantité de mouvement d'un objet qui se déplacerait à la vitesse de la lumière serait donc infinie, et donc pour qu'un vaisseau puisse atteindre la vitesse de la lumière, il faut lui communiquer une quantité de mouvement infinie..... pas facile!!.

Vous entendrez peut-être dire qu'en approchant de la vitesse de la lumière, la masse d'un objet augmente pour atteindre l'infini à la vitesse C, c'est inexacte car la masse est ce que l'on appelle un invariant relativiste, ce qui signifie qu'elle ne change pas avec la vitesse, par contre, puisque la quantité de mouvement, elle, devient infinie, tout se passe COMME si la masse était devenue infinie, mais seulement comme.

2) L'énergie cinétique:

Vous connaissez la formule E=1/2mv², donnant l'énergie cinétique d'un mobile.

Comme vous vous en doutez, et comme pour la quantité de mouvement, cette formule n'est pas valable en mécanique relativiste.

Vous connaissez sans doute déja la formule légendaire donnant l'énergie que l'on pourrait obtenir en provoquant la désintégration totale d'une masse m donnée, et qui est: E=mc², cette formule donne donc l'énergie au repos, c'est à dire à vitesse nulle.

Si l'objet se déplace, il faut tenir compte du supplément d'énergie du à la vitesse.
La formule donnant l'énergie totale d'un corps en mécanique relativiste est:

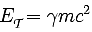. Tiens, revoilà le gamma relativiste!

L'énergie totale, c'est l'énergie cinétique + l'énergie au repos; donc l'énergie cinétique, c'est l'énergie totale moins l'énergie au repos.

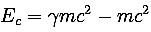En mettant mc² en évidence, on a: .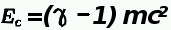

Et puisque: 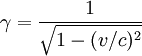, alors, l'expression de l'énergie cinétique en mécanique relativiste devient:

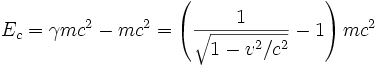Même remarque que pour la quantité de mouvement, si v=c, alors v²/c²=1, et 1-v²/c²=0. dans ce cas le dénominateur s'annule et la fraction prend une valeur infinie à laquelle le -1 ne peut, bien sûr, rien changer.

Un objet voyageant à la vitesse de la lumière possède donc une énergie cinétique infinie. Cette énergie cinétique infinie, il a bien fallu la lui donner.

Conclusion: pour propulser un vaisseau jusqu'à la vitesse de la lumière, il faut lui communiquer une énergie infinie!

Voilà pourquoi, non seulement la vitesse de la lumière ne peut être dépassée, mais elle ne peut pas non plus être atteinte par quoique ce soit qui possède une masse.

Entre le repos où l'énergie est minimale, et la vitesse de la lumière (C) où l'énergie est infinie, il y a place pour toutes les valeurs d'énergie intermédiaires dont certaines peuvent être astronomiques.

Plus on se rapproche de la vitesse de la lumière (C), plus l'énergie nécessaire à gagner encore un peu de vitesse devient "énormissime". L'energie requise augmente, par rapport à la vitesse, selon une courbe de ce genre:

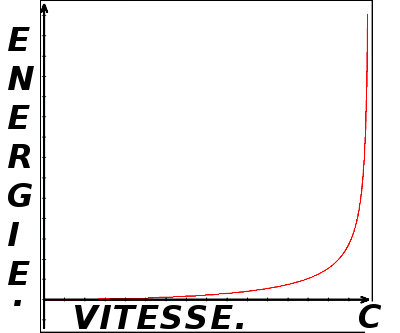
Comme vous pouvez le constater, c'est seulement à l'approche de la vitesse de la lumière (C) que l'énergie augmente vite par rapport à la vitesse (la courbe se "dresse") et ensuite, à toute augmentation, même modeste, de la vitesse, correspond une augmentation énorme de l'énergie, pour atteindre l'infini à C.

maginez un vaisseau dont la vitesse est si proche de C que son énergie est comparable à celle dégagée par toutes les étoiles d'une galaxie entière pendant un milliard d'années (on ne dit pas comment il a été possible de lui fournir tout ça!!).

Compte tenu de la croissance de la courbe d'énergie, il pourrait consommer l'équivalent de milliers de galaxies supplémentaires sans accélérer significativement. Choquant? Je vais en reparler un peu plus loin.

J'ai volontairement pris un exemple extrême, où l'énergie est vraiment énorme.

Maintenant, comparons la à l'énergie cinétique d'un vaisseau de 100 tonnes volant à 99% de C, elle est d'environ 55 milles milliards de milliards de joules, soit l'énergie produite par une centrale nucléaire d'un gigawatt pendant environ 180.000 ans; c'est beaucoup, mais loin de l'énergie de plusieurs galaxies, et encore bien loin de l'infini.

Que nous montre cette comparaison?

Qu'un vaisseau qui s'approche de la vitesse de la lumière, et dont l'énergie atteint "seulement", si l'on peut dire, 55 milles milliards de milliards de joules alors qu'il se déplace déjà à 99% de C atteindra des valeurs d'énergie totalement inimaginables (jusqu'à atteindre celles de plusieurs galaxies) dans le dernier pour cent avant C!

Cela illustre bien l'extraordinaire vitesse de croissance de l'énergie à proximité de la vitesse de la lumière.

J’ai dit plus haut qu’un vaisseau dont la vitesse est si proche de C que son énergie est comparable à celle dégagée par toutes les étoiles d'une galaxie entière pendant un milliard d'années pourrait consommer l'équivalent de milliers de galaxies supplémentaires sans accélérer significativement.

On retrouve d’ailleurs le même «phénomène» dans les accélérateurs de particules. Si on a des protons qui circulent déjà à 99,9% de la vitesse de la lumière et que l’on DOUBLE l’énergie qu’on leur apporte, leur vitesse ne variera que d’un infime «pouillème», mais leur énergie aura RÉELLEMENT doublé...

Faut-il croire alors qu’un supplément de poussée sur un vaisseau qui se déplace déjà à 99% de la vitesse de la lumière n’a strictement aucun effet? Ce serait illogique….

En fait ce sont les effets relativistes tels que la contraction des distances ou le ralentissement de l'écoulement du temps (expression trompeuse, mais populaire*), seraient, par contre, nettement augmentés.

(*) Pour une expression plus conforme à la réalité, il faut parler de dilatation du temps….. lorsqu’il est mesuré par un observateur extérieur….. En fait, les passagers du vaisseau ne remarquent rien dans leur fusée, tandis qu’un observateur terrien, par exemple, mesurera chez eux des secondes plus longues (dilatée) si il peut vois une horloge dans la fusée. Parallèlement, les passagers de la fusée verront les horloges ralentir sur Terre, mais les terriens….non..

Ce sont CES EFFETS RELATIVISTES LÀ (contraction des distances, dilatation du temps) qui s’accroissent brutalement, et à la place de la vitesse, si les astronautes décident d’accélérer….. Et avec, en prime, tout de même la sensation d’accélérer..

Est-ce à dire que s’ils accélèrent, ils ressentent «des g» mais ne voient aucun changement en regardant dehors?

Non, au contraire, ils verront une contraction des distances qui leur apparaîtra bien semblable à une «vraie» accélération.

C’est seulement les observateurs extérieurs qui ne les «accompagnent» pas dans leur mouvement qui verront la fusée ne (pratiquement) pas accélérer malgré les moteurs à fond (par contre, ils mesureront une forte augmentation de la dilatation du temps pour les astronautes..).

La contraction des distances signifie qu’en s'approchant de la vitesse de la lumière, l'équipage du vaisseau aurait l'impression de voir l'univers "s'écraser" dans le sens du déplacement, et donc les distances fondrent littéralement.

Ce phénomène serait, pour eux, et seulement pour eux, l'explication de la brièveté de leur voyage.

Pour faire la part des choses entre astronautes et observateurs terriens, disons que les occupants du vaisseau "verraient" l'univers rétrécir dans le sens du déplacement, mais PAS leur vaisseau; tandis qu'un observateur «terrien» "verrait" le vaisseau rétrécir mais PAS l'univers.

Ci dessous, trois images, illustrant la contraction des distances….. En y mélangeant les points de vue «astronautes» (contraction des distances hors de la fusée), et «terriens» (contraction de la longueur de la fusée).

En fait, j'ai juste rétrécis l'image dans le sens de la longueur, et donc, tout a rétréci ensemble.

L'autre effet relativiste le plus connu, est donc la dilatation du temps.

Exemple:

Une seconde pour les occupants du vaisseau serait, au départ, égal à une seconde pour les copains restés sur Terre, mais au fur et à mesure que les effets relativistes se feraient sentir (en s'approchant de la vitesse C), une seconde pour les occupants du vaisseau deviendrait égal à une minute, puis une heure, un jour, un mois, ou même une année terrestre en se rapprochant de plus en plus de C.

C'est là l'explication du vieillissement plus faible pour les occupants du vaisseau que pour les copains restés sur Terre, n'ayant subi aucun effets relativistes, qui eux auraient vieillis du temps correspondant à la simple division de la distance réelle à parcourir par la vitesse réelle du vaisseau, et cela peut signifier des millénaires!!!.

C’est à ce moment là, en général, que quelqu’un se dit: "mais le mouvement est relatif, et donc on peut dire que c’est plutôt la Terre qui s’éloigne et la fusée qui ne bouge pas (c’est d’ailleurs le cas dans le référentiel de la fusée). Et donc dans ce cas, pourquoi n’est-ce pas la Terre qui vieillit moins vite que les astronautes dans leur fusée?"

C’est qu’en réalité les deux situations ne sont pas symétriques.

Si l’on reprend le scénario habituel des jumeaux dont l’un reste sur Terre tandis que l’autre voyage, alors le premier reste continuellement dans le même référentiel (la Terre) dans lequel aucun changement ne se produit, tandis que l’autre change de référentiel (grâce à ses* accélérations*). Ou pour le dire autrement, le jumeau terrien est PASSIF pendant toute la durée du voyage, le jumeau astronaute, accélère, tourne, revient, bref il a un rôle ACTIF dans cette histoire et c’est ça qui supprime la symétrie.

(*) Au départ, puis lors du demi tour, et encore une fois de plus au retour.

Pour être très précis, c’est au moment du demi tour (inversion du sens de déplacement) que tout bascule pour le jumeau dans la fusée, mais l’explication complète serait trop longue (et compliquée) pour être donnée ici.

Par contre, il existe une expérience de pensée qui permet de facilement comprendre que les deux situations (jumeau sur Terre et jumeau dans la fusée) sont différentes, et la voici.

Imaginons que les deux jumeaux aient convenu d’émettre, l’un vers l’autre (par radio) un «bip» répétitif, avec un rythme d’un par seconde.

Je crois qu’il est assez facile de comprendre que:

-Si le jumeau voyageur émet un bip chaque seconde (pour lui), le jumeau resté sur Terre les recevra avec un écart supérieur à une seconde puisque, du fait de l’éloignement continu de la fusée, chaque bip est émis par la fusée depuis un peu plus loin à chaque fois.

-Si le jumeau resté sur Terre émet un bip chaque seconde (pour lui), le jumeau voyageur les recevra avec un écart supérieur à une seconde puisque, du fait de l’éloignement continu de la fusée, chaque bip émis depuis la Terre a un peu plus de distance à parcourir à chaque fois pour rejoindre la fusée qui, rappelons le, s’éloigne.

Pendant toute la durée de l’accélération de la fusée, l’écart entre chaque «bip» ne cesse d’augmenter, et cela aussi bien pour le jumeau voyageur que pour celui resté sur Terre.

Dès que l’accélération cesse, la durée entre les «bips» reste bien sûr supérieure à une seconde (puisque la fusée continue de s’éloigner) mais elle cesse d’augmenter……. Pour le voyageur uniquement!!!!!!

Pourquoi? Parce que le jumeau resté sur Terre devra attendre l’arrivée des premiers «bips» émis juste après l’arrêt de l’accélération. Ces premiers «bips» doivent parcourir la distance entre la fusée au moment de leur émission, et la Terre, or ça peut prendre beaucoup de temps (5 ans si l'on imagine un voyage vers une étoile située à une dizaine d'années lumière, et que l’arrêt de l’accélération se produit à mi chemin).

Du côté du voyageur, les choses sont différentes. Lui, en quelque sorte, «baigne» dans les ondes émises (et donc les «bips» émis) par la Terre depuis son départ. Ces ondes sont toutes pareilles et la modification du rythme apparent de réception n’est en rien lié à quelque chose se produisant sur Terre, mais uniquement à la poursuite ou non de l’accélération de la fusée donc au fonctionnement de son moteur, donc à un phénomène local et une décision locale.

Conséquence: la modification du rythme de réception apparaît immédiatement après la fin de l’accélération pour le voyageur, pas pour son frère.

Le jumeau voyageur continue donc et fait demi tour.

Lors de ce demi-tour, les ondes en provenance de la Terre n’ont pas changé. Par contre, de par la manœuvre décidée et réalisée par le voyageur uniquement, ces ondes, désormais, il les rencontre de face.

C’est comme un bateau qui navigue d’abord dans le sens des vagues puis qui fait demi tour, et désormais, sans qu’il y ait eu modification réelle de l’écart entre les vagues, les traverse de manière plus rapprochée parce qu’il va désormais à leur rencontre.

Oui mais, me direz vous, pour les vagues, pas de problème puisque après le demi tour, la vitesse relative entre les vagues et le bateau a logiquement augmenté, mais pour les ondes radio c’est différent puisque la relativité impose une vitesse invariante «c».

Certes, mais le seul fait que la fusée se déplace à une certaine vitesse vers la Terre, fait que la distance restante diminue constamment et donc la distance à parcourir par les ondes (ou vagues, ou «bips») diminue elle aussi constamment, et en conséquence la distance entre deux «bips» dimminue de la même manière.

C’est pour ça que, même si la vitesse de ces ondes est invariante, la durée entre deux bips a diminué dès le demi tour.

Par contre, pour le jumeau resté sur Terre, c’est différent. Lui ne se déplace pas activement en direction des ondes.

Pour lui, qui est passif, il n’est possible de constater une accélération du rythme que lorsqu’il recevra les ondes que la fusée a émises en se déplaçant vers la Terre (donc APRÈS le demi tour, plus le temps pour qu’elles arrivent).

C’est parce que, après le demi-tour, la fusée se déplace vers la Terre à une certaine vitesse que la distance d’émission diminue constamment entre deux «bips» et c’est ça qui donne l’augmentation du rythme.

Mais pour recevoir ces ondes émises après le demi-tour, il faut qu’elles aient fait tout le trajet depuis l’étoile où le demi-tour a été réalisé, et, dans l’exemple choisi, ça prend dix ans…….…

Pour la fusée, le rythme apparent d’émission des «bips» augmente donc juste après le demi-tour parce que le déplacement de la fusée fait constamment diminuer la distance restante avec la Terre, et donc le temps nécessaire pour le trajet de chaque «bips» consécutif.

Mais le jumeau resté sur Terre ne peut constater cette augmentation de rythme que lorsque les ondes émises depuis le demi tour, seront parvenues sur Terre, donc dix ans.

Il y a donc bien une assymétrie entre les deux jumeaux.

Le jumeau voyageur constate une augmentation du rythme des «bips» dès son demi-tour, et donc tout au long de son voyage de retour, alors que le jumeau resté sur Terre ne constatera cette augmentation que dix ans plus tard (selon SON calendrier), et si le jumeau voyageur va vraiment très vite, cette augmentation du rythme précédera de peu le retour de son frère.

Ou pour le dire autrement: Le jumeau voyageur voit les messages de son frère lui parvenir au ralenti pendant la moitié du voyage et en accéléré pendant l’autre moitié du voyage, tandis que le jumeau resté sur Terre voit les messages de son frère lui parvenir au ralenti pendant la très très grande majorité du voyage et en accéléré seulement pendant un temps assez bref, à la fin.

Conclusion: Si chaque jumeau utilise le rythme des «bips» reçus pour estimer le temps qui passe chez son frère, le jumeau voyageur se dira que son frère a vieilli lentement pendant la moitié du voyage et vite pendant l’autre moitié, tandis que le jumeau resté sur Terre se dira que son frère voyageur a vieilli lentement pendant presque tout le voyage et vite pendant très peu de temps à la fin.

Sans même avoir tout à fait atteint la vitesse de la lumière un vaisseau peut (doit) donc posséder une énergie incommensurable, totalement incompatible avec quelque technologie que ce soit, ce qui exclu toute possibilité même lointaine de parvenir à voyager à de telles vitesses.

Pour que le voyage intersidéral soit possible un jour, il faudra trouver autre chose...

C'est ainsi que des hypothèses concernant d'autres façons de voyager dans l'univers ont été proposées. Ce ne sont que des hypothèses non encore vérifiées, mais je vais quand même en parler.......pour préserver le rêve!!

Nous allons donc parler de Warp Drive, de voyage passant par les "trous de vers", et autres manipulations de l'espace-temps..... mais..... sans illusions.