Avant de poursuivre sur les applications, un p'tit rappel concernant les groupements de condensateurs:

Plaçons plusieurs condensateurs "en parrallèle", comme sur le dessin ci dessous.

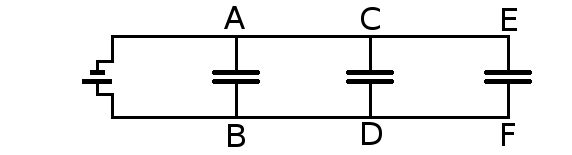
Tous les condensateurs sont soumis à la même tension, puisque A, C et E sont reliés ensemble et directement à la borne négative du générateur, et que B, D et F sont eux aussi reliés ensemble et directement à la borne positive du générateur.

La charge d'un condensateur est égale à sa capacité multipliée par la tension à laquelle il est soumis; donc Q = C*U.

Chaque condensateur peut avoir une capacité (C) différente de celles des autres, on appellera donc C1 la capacité du premier condensateur, C2 la capacité du second, et C3 celle du troisième.

La tension U est par contre strictement la même pour les trois condensateurs, on la désignera donc chaque fois de la même manière, par U.

La charge du premier condensateur est donc: Q1 = C1 * U.
La charge du deuxième condensateur est donc: Q2 = C2 * U.
La charge du troisième condensateur est donc: Q3 = C3 * U.

On désignera par I1 le courant qui charge le premier condensateur.
On désignera par I2 le courant qui charge le deuxième condensateur.
On désignera par I3 le courant qui charge le troisième condensateur.
Le courant total délivré par le générateur est la somme de ces trois courants.

Une charge, c'est une quantité d'éléctricité, et une intensité (un courant), c'est un débit d'éléctricité, donc une charge par unité de temps.

Conséquence: de la même façon que le courant total délivré par le générateur est égal à la somme des courants de charge de chaque condensateur, la charge totale du système (Qtot) est égale à la sommes des charges des trois condensateurs (Q1, Q2 et Q3).

En d'autres termes: Qtot = Q1 + Q2 + Q3.
Puisque Q = C*U, on a:
Qtot = (C1*U)+(C2*U)+(C3*U).
Donc Qtot = (C1+C2+C3)*U.
La charge totale (Qtot) est égale à la capacité totale (Ctot) multipliée par la tension U.
Donc Qtot = Ctot*U.
Mais puisque Qtot = (C1+C2+C3)*U.
On en déduit que Ctot*U = (C1+C2+C3)*U, donc que Ctot = C1+C2+C3.

En d'autre termes:
la capacité totale équivalente de plusieurs condensateurs placés en parallèle est égale à la somme des capacités des condensateurs.

On peut donc remplacer, dans presque tous les cas (eh oui, il y a toujours des exceptions, on en reparlera à la page suivante), plusieurs condensateurs placés en parallèle par un seul de capacité équivalente.

Que se passe-t'il si les condensateurs sont placés en série (c'est à dire "à la queue leu leu") plutôt qu'en parallèle?

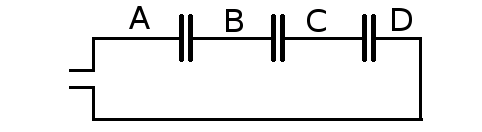
Pendant la charge (ou si la tension d'alimentation est alternative), il y a passage d'un courant.
Tous les condensateurs sont "traversés" par le même courant, puisqu'ils se suivent et que le courant qui "traverse" l'un doit forcément "traverser" aussi les autres.

Etant donné qu'il recoivent tous le même courant pendant le même temps, ils recoivent tous la même charge, et ont donc tous la même charge.

La charge totale du système est, elle aussi strictement égale à la charge de chaque condensateur puisque on a le même courant pendant le même temps dans l'ensemble du système!

Donc: Qtot = Q1 = Q2 = Q3.

Chaque condensateur peut avoir une capacité (C) différente de celles des autres, on appellera donc C1 la capacité du premier condensateur, C2 la capacité du second, et C3 celle du troisième.

Chaque condensateur peut être soumis à une tension différente de celles des autres (c'est même inévitable si les capacités sont différentes alors que la charge est la même puisque: Q=C*U), on appellera donc U1 la tension du premier condensateur, U2 la tension du second, et U3 celle du troisième.

Puisque Qtot = Q1 = Q2 = Q3, et que la charge est le produit de la capacité par la tension, on a:
Qtot = Ctot*U = C1*U1 = C2*U2 = C3*U3.

La tension totale U (donc entre A et D) est égale à la somme des tensions partielles U1, U2 et U3, donc U = U1 + U2 + U3.

Puisque Q=C*U, alors U=Q/C et U1=Q/C1, U2=Q/C2, et U3=Q/C3 (toujours le même Q puisque Q1=Q2=Q3).

U=U1+U2+U3 devient: Q/Ctot = Q/C1 + Q/C2 + Q/C3.

En divisant les deux membres par Q, il vient: 1/Ctot = 1/C1 + 1/C2 + 1/C3.

Dans le cas de condensateurs en série, l'inverse de la capacité totale équivalente est égal à la somme des inverses des capacités de chaque condensateurs.

On le sait maintenant, un condensateur soumis à une tension alternative, ou tout au moins variable, agit comme s'il était conducteur.

Cette "conductibilité" n'est pas (presque) parfaite comme celle d'un simple fil, sa valeur dépend de la capacité du condensateur (C) et de la vitesse de variation de la tension qui lui est appliquée.

L'influence de la capacité du condensateur sur cette "conductibilité" peut se comprendre aisément.
On a dit plus haut qu'il y avait équivalence entre plusieurs condensateurs placés en parallèle et un seul condensateur d'une capacité équivalente (à la somme des capacités).

Imaginons donc un circuit comprenant un condensateur et alimenté par une tension alternative. Ce circuit est le siège d'un courant d'une certaine valeur.

Ajoutons un deuxième condensateur de même valeur en parallèle. Etant placé en parallèle, il sera soumis à la même tension que le premier, et puisque je l'ai choisi de même capacité, il laissera passer un courant de même intensité.

En doublant le nombre de condensateurs j'ai doublé la capacité totale, mais j'ai aussi doublé le courant.

Ajoutons un troisième condensateur, toujours de même valeur, toujours en parallèle, et voilà qu'en triplant la capacité j'ai triplé aussi l'intensité.

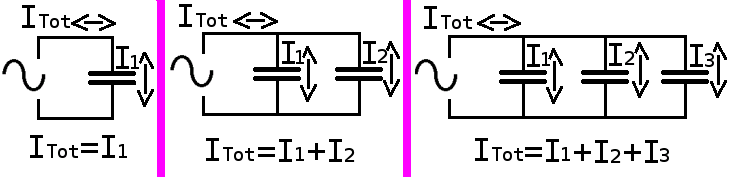
On sait maintenant qu'en multipliant les condensateurs en parallèle, je n'ai fait que multiplier la capacité totale du système, et multiplier le courant de la même façon.

Il y a donc une stricte équivalence entre rajouter plusieurs condensateurs ou remplacer par un seul d'une capacité plus grande, le résultat est le même: une augmentation de l'intensité du courant.

En résumé: plus la capacité est grande plus le courant est fort, la conductibilité est donc directement proportionnelle à la capacité.

Pour montrer l'influence de la vitesse de variation de tension sur cette "conductibilité" des condensateurs, il y a deux voies:

La première, presqu'intuitive, peut se déduire d'expériences simples:

1) On branche notre circuit comprenant un condensateur et une résistance directement sur une source de tension (une batterie, par exemple).

Le circuit est immédiatement soumis à la tension du générateur (12 volts pour une batterie).

Pendant la charge, la tension aux bornes du condensateur augmente alors selon cette courbe désormais connue:

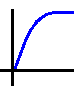
2) Reprenons le même circuit et branchons le sur un générateur équipé d'un système permettant de régler la tension à volonté.

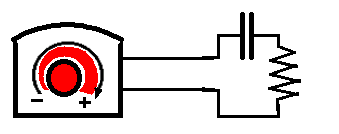
La tension, nulle au départ, est portée à 12 volts en tournant le "beau gros bouton rouge" prévu à cet effet sur mon générateur.

La tension s'installe donc beaucoup plus progressivement (dépendant de la vitesse avec laquelle le bouton est manipulé) que dans le cas précédent.

Si l'installation de la tension dans le circuit se fait de manière plus progressive, il est normal d'en déduire que l'augmentation de la tension aux bornes du condensateur sera plus lente.

La tension aux bornes du condensateur est l'image de son niveau de charge, si donc cette tension augmente plus lentement, cela signifie forcément que la charge se fait plus lentement.

Si le condensateur se charge plus lentement c'est qu'il reçoit un débit de charge plus faible.

Le débit de charge, c'est justement l'intensité; il y a donc bien un lien directe entre la vitesse de variation de la tension et l'intensité qui "traverse" un condensateur.

A tension égale, si l'intensité est plus grande, c'est que le courant circule plus facilement, donc que la conductibilité est meilleure.

La deuxième façon de montrer le lien entre la vitesse de variation de la tension et la "conductibilité" d'un condensateur est un peu plus "physico-mathématique". Elle découle de la définition même de l'intensité qui est un débit de charge électrique, donc une variation de charge par rapport au temps que l'on peut écrire sous la forme de: I=dq/dt.

Puisque: Q=C*U, il vient: I=dq/dt=C*du/dt.

du/dt c'est la variation de la tension par rapport au temps, donc c'est la vitesse de variation de la tension.

Par conséquent, l'intensité du courant qui "traverse" un condensateur est directement proportionnelle à la vitesse de variation de la tension d'alimentation.

Rappelons encore qu'à tension égale, si l'intensité est plus grande, c'est que le courant circule plus facilement, donc que la conductibilité est meilleure.

On a, jusqu'ici, employé ce terme de "conductibilité" pour désigner la facilité avec laquelle le courant peut passer, mais en électricité on parle plutôt de résistance qui est, au contraire, l'aptitude à s'opposer au passage du courant.

La résistance est donc l'aptitude à s'opposer au passage du courant, mais de la même manière exactement que l'on soit en présence d'un courant continu, variable (et quelque soit la vitesse de variation), pulsé, ou carrément alternatif (et quelque soit sa fréquence).

Ce n'est pas le cas pour un condensateur où l'opposition au passage du courant est très différente selon que l'on soit en présence d'un courant continu ou alternatif.

Pour éviter toute confusion, on choisira un autre terme, celui d'impédance.

L'impédance est donc l'aptitude à s'opposer au passage d'un courant alternatif sinusoïdal.

On a dit que la facilité avec laquelle un condensateur laisser passer un courant alternatif est directement proportionnelle à la capacité du condensateur et à la vitesse de variation de la tension.

A l'inverse, l'impédance d'un condensateur est donc inversément proportionnelle à la capacité du condensateur et à la vitesse de variation de la tension.

L'équivalent de la vitesse de variation de la tension pour un courant alternatif, c'est la fréquence(f), ou plutôt ce que l'on appelle la pulsation et qui vaut 2*Pi*f, donc deux fois pi fois la fréquence.

Le dessin ci dessous montre, à gauche, le mouvement circulaire dans le sens trigonométrique, d'un segment de droite (représenté successivement en jaune, mauve, vert, rouge, et ocre).

On projette, sur l'axe des ordonnées, l'extrémité du segment de droite aux temps t1, t2, t3, t4, et t5 et on obtient respectivement les point a, b, c, d, et e.

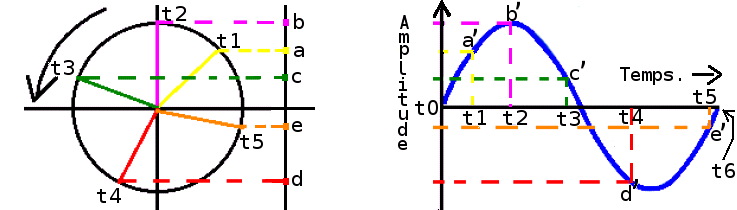
A droite, on trace un repère orthonormé dans lequel on place, en correspondance avec le dessin de gauche, les points a', b', c', d' et e', correspondant aux amplitudes a, b, c, d, et e atteintes aux temps t1, t2, t3, t4, et t5.

La courbe obtenue en joignant tous ces points est une sinusoïde.

La distance de temps qui sépare t0 et t6 sur le dessin de droite s'appelle la période, mais c'est aussi la durée d'un tour complet du segment sur le dessin de gauche.

La fréquence d'une onde est égale au nombre de période par seconde, elle est donc aussi égale au nombre de tour par seconde du segment sur le dessin de gauche.

Un tour complet sur un cercle est égal à un angle de deux pi (radians).
En multipliant deux pi (tour complet) par la fréquence (nombre de périodes mais aussi nombre de tour par seconde) on obtient la vitesse angulaire du segment qui est l'image de la vitesse de variation de la courbe sinusoïdale du dessin de droite.

Ce produit 2*pi*f est donc la plulsation, et c'est précisément cette pulsation qui représentera la vitesse de variation de la tension dans le calcul de l'impédance d'un condensateur soumis à une tension alternative.

Conclusion: puisque l'impédance (Z) d'un condensateur soumis à une tension alternative est inversément proportionnelle (donc 1/quelque chose) à la capacité (C) et à la pulsation (oméga, que l'on représentera ici pour la facilité par la lettre W), on a: Z=1/CW.

Attention, si l'on a une résistance et un condensateur en série (donc qui se suivent), on ne peut pas additionner simplement la résistance et l'impédance du condensateur pour obtenir l'impédance totale du circuit.

En fait, l'impédance totale d'un circuit résistance + condensateur en série s'exprime comme ceci:
Z = racine carrée de (R² + 1/(c*w)²).